Câu hỏi:
2 năm trước
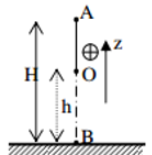
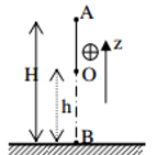
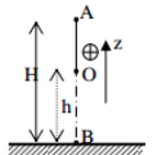
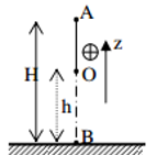
Một vật có khối lượng \(m = 2kg\) được thả rơi tự do từ độ cao \(h = 45m\) so với mặt đất. Lấy \(g = 10m/{s^2}\).
a) Chọn mốc thế năng ở mặt đất và chiều dương hướng lên, viết biểu thức động năng và thế năng của vật tại vị trí có độ cao \(z\) so với mặt đất.
b) Tìm vị trí mà tại đó vật có động năng bằng nửa thế năng.
Trả lời bởi giáo viên
Đáp án đúng: c
a) Biểu thức động năng và thế năng của vật tại vị trí có độ cao z so với mặt đất:
\(\left\{ \begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2}\\{W_t} = mgz\end{array} \right.\)
Với \(v\) là vận tốc của vật tại vị trí có độ cao\(z\).
b) + Vị trí vật được thả rơi có: \(\left\{ \begin{array}{l}{v_0} = 0\\{h_0} = 45m\end{array} \right.\)
Cơ năng tại đó: \({W_0} = {W_d} + {W_t} = mg{h_0}\)
+ Tại vị trí động năng bằng nửa thế năng: \({W_d} = \dfrac{1}{2}{W_t}\) có cơ năng:
\(W = \dfrac{1}{2}{W_t}\, + {W_t} = \dfrac{3}{2}{W_t} = 1,5.mgh\)
+ Áp dụng định luật bảo toàn cơ năng ta có:
\({W_0} = W \Leftrightarrow 1,5.mgh = mg{h_0} \Rightarrow h = \dfrac{{{h_0}}}{{1,5}} = \dfrac{{45}}{{1,5}} = 30m\)
Hướng dẫn giải:
+ Biểu thức động năng, thế năng trọng trường: \(\left\{ \begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2}\\{W_t} = mgz\end{array} \right.\)
+ Cơ năng của vật chuyển động trong trọng trường: \(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + mgz\)
+ Định luật bảo toàn cơ năng: Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn.
