Câu hỏi:
1 năm trước
Một thanh AB dài 2m khối lượng m = 2kg được giữ nghiêng một góc \(\alpha \) trên mặt sàn nằm ngang bằng một sợi dây nằm ngang BC dài 2m nối đầu B của thanh với một bức tường đứng thẳng; đầu A của thanh tựa lên mặt sàn. Hệ số ma sát giữa thanh và mặt sàn bằng \(\frac{{\sqrt 3 }}{2}\). Các giá trị của \(\alpha \) để thanh có thể cân bằng.
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
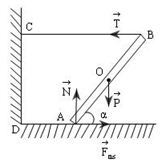
Xét tâm quay tại A, ta có
+ Áp dụng quy tắc momen, ta có: \({M_P} = {M_T}\)
+ Mặt khác: \(\left\{ \begin{array}{l}{M_P} = P.AO.c{\rm{os}}\alpha = P.\frac{{AB}}{2}.c{\rm{os}}\alpha \\{M_T} = T.AB.\sin \alpha \end{array} \right.\)
Ta suy ra:
\(\begin{array}{l}P.\frac{{AB}}{2}{\rm{cos}}\alpha {\rm{ = T}}{\rm{.AB}}{\rm{.}}\sin \alpha \\ \to T = 0,5P.cot\alpha \end{array}\)
Theo phương ngang, để thanh cân bằng thì
\(\begin{array}{l}{F_{m{\rm{s}}}} \le T \leftrightarrow \mu mg \le 0,5mg.\cot \alpha \\ \to \cot \alpha \ge \sqrt 3 \to \alpha \ge {30^0}\end{array}\)
Hướng dẫn giải:
+ Vận dụng quy tắc momen: \({M_1} + {M_2} + ... = 0\)
+ Vận dụng biểu thức tính momen của lực: \(M = F{\rm{d}}\)
Câu hỏi khác
- Bài tập trắc nghiệm Định luật 3 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Trọng lực và lực căng môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Định luật 2 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Tổng hợp và phân tích lực. Cân bằng lực môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Định luật 1 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
