Một sợi dây căng ngang với hai đầu cố định, đang có sóng dừng. Biết khoảng cách xa nhất giữa hai phần tử dây dao động với cùng biên độ 5 mm là 80 cm, còn khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha với cùng biên độ 5 mm là 65 cm. Tỉ số giữa tốc độ cực đại của một phần tử dây tại bụng sóng và tốc độ truyền sóng trên dây là
Trả lời bởi giáo viên
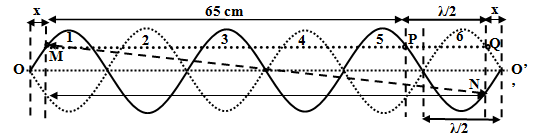
+ Các điểm thuộc cùng một bó sóng dao động cùng pha nhau, các điểm thuộc bó sóng lẻ dao động ngược pha với các điểm thuộc bó sóng chẵn.
+ Khoảng cách xa nhất giữa hai phần tử dây dao động cùng biên độ 5 mm ở hai bó sóng ngoài cùng (cùng cách mỗi đầu cố định một khoảng x) là: MN = 80cm.
+ Khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha cùng biên độ 5 mm là: MP = 65 cm.
+ Dễ dàng nhận thấy: \(PQ = \dfrac{\lambda }{2}\)
=> \(PQ = \dfrac{\lambda }{2} = MQ - MP = \sqrt {M{N^2} - Q{N^2}} - MP = \sqrt {{{80}^2} - {1^2}} - 65 \approx 15cm = > \lambda \approx 30cm.\)
+ Ta có \((MQ = 79,99 \approx 80cm)\) (: \(\dfrac{{MQ}}{{\lambda /2}} = \dfrac{{80}}{{15}} = 5 + \dfrac{1}{3}\)
=> Trên sợi dây có 6 bó sóng. (Có \(\dfrac{1}{3}.\dfrac{\lambda }{2} + 2x = \dfrac{\lambda }{2})\)
+ Chiều dài sợi dây là: \(\ell = OO' = \dfrac{\lambda }{2} = 90cm \Rightarrow x = \dfrac{{OO' - MQ}}{2} = \dfrac{{90 - 80}}{2} = 5cm.\)
+ Biên độ sóng tại điểm M cách nút sóng 1 khoảng x là: \({A_M} = 2.a\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| = 2a.\sin \dfrac{{2\pi .5}}{{30}} = a\sqrt 3 = 5mm.\)
=> \(a = \dfrac{{0,5}}{{\sqrt 3 }}(cm)\)
=> Biên độ bụng sóng là: \(2a = \dfrac{1}{{\sqrt 3 }}(cm)\)
+ Tốc độ cực đại của phần tử tại bụng sóng: vmax = 2aω = \(\dfrac{1}{{\sqrt 3 }}\)2πf (cm/s).
+ Tốc độ truyền sóng trên dây: \(v = λf = 30f (cm/s)\)
+ Tỉ số: \(\dfrac{{{v_{\max }}}}{v} = \dfrac{{2\pi }}{{\sqrt 3 .30}} \approx \)\(0,12086\).
Hướng dẫn giải:
Sử dụng lí thuyết về sóng dừng trên dây hai đầu cố định

