Câu hỏi:
3 năm trước
Một quả tạ được ném lên từ một vận động viên ném tạ chuyển động với phương trình \(y = - 0,0241{x^2} + x + 5,5\) trong đó x là độ xa và y là độ cao (tính bằng feet). Hỏi vận động viên ném được xa nhất là bao nhiêu feet?
Chỉ điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
Gọi A là giao điểm có hoành độ dương của parabol (P): \(y = - 0,0241{x^2} + x + 5,5\) với trục hoành
B là điểm cao nhất của đồ thị như hình vẽ
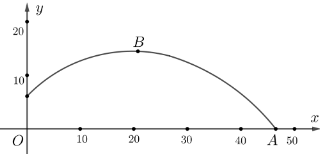
Bài toán trở thành: tìm hoành độ x của A và tung độ y của B.
Phương trình hoành độ giao điểm của (P) và trục hoành: \( - 0,0241{x^2} + x + 5,5 = 0\) có hai nghiệm, trong đó nghiệm dương là \(x = 46\)
Khi đó điểm xa nhất là 46 feet.
Hướng dẫn giải:
Đưa bài toán về bài toán tìm giao điểm của (P) và trục hoành.


