Một ôtô chuyển động trên đoạn đường thẳng. Trong $1/2$ quãng đường đầu đi với vận tốc $40km/h$ , trong $1/2$ quãng đường còn lại ôtô đi với vận tốc như sau: trong $1/2$ thời gian đầu với vận tốc $75km/h$ và trong $1/2$ thời gian cuối với vận tốc $45km/h$. Tốc độ trung bình trên đoạn đường là:
Trả lời bởi giáo viên
Ta có:
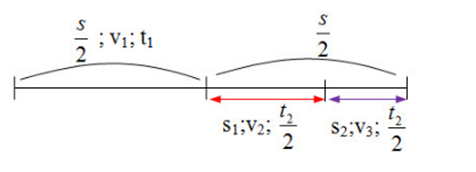
\(\begin{array}{l}{t_1} = \dfrac{{\dfrac{s}{2}}}{{{v_1}}} = \dfrac{s}{{80}}\\\dfrac{{{t_2}}}{2} = \dfrac{s_1}{{v{}_2}} = \dfrac{s_2}{v_3} \to 3{{\rm{s}}_1} = 5{{\rm{s}}_2}\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{s_1} + {s_2} = \dfrac{s}{2}\\ \to {s_1} = \dfrac{{5{\rm{s}}}}{{16}};{s_2} = \dfrac{{3{\rm{s}}}}{{16}}\\ \to {t_2} = \dfrac{{2{{\rm{s}}_1}}}{{{v_2}}} = \dfrac{{5{\rm{s}}}}{{8{v_2}}} = \dfrac{s}{{120}}\\{v_{tb}} = \dfrac{s}{{{t_1} + {t_2}}} = \dfrac{s}{{\dfrac{s}{{80}} + \dfrac{s}{{120}}}} = 48km/h\end{array}\)
Hướng dẫn giải:
Vận dụng biểu thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{s}{t}\)

