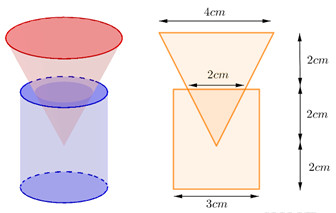
Một nút chai thủy tinh là một khối tròn xoay \(\left( H \right)\), một mặt phẳng chứa trục của \(\left( H \right)\) cắt \(\left( H \right)\) theo một thiết diện như trong hình vẽ bên dưới. Tính thể tích \(V\) của \(\left( H \right)\).
Trả lời bởi giáo viên
Hình \(\left( H \right)\) bao gồm:
+ Khối trụ có bán kính đáy \({R_1} = \dfrac{3}{2}\,\,\left( {cm} \right)\), chiều cao \(h = 4\,\,\left( {cm} \right) \Rightarrow \) Thể tích của khối trụ là: \({V_1} = \pi .{\left( {\dfrac{3}{2}} \right)^2}.4 = 9\pi \,\,\left( {c{m^3}} \right)\).
+ Khối nón cụt có hai bán kính đáy là \({r_2} = \dfrac{2}{2} = 1\,\,\left( {cm} \right),\,\,{R_2} = \dfrac{4}{2} = 2\,\,\left( {cm} \right)\) và chiều cao \(h' = 2\,\,\left( {cm} \right)\) \(\) Thể tích nón cụt là: \({V_2} = \dfrac{1}{3}\pi .\left( {{1^2} + 1.2 + {2^2}} \right).2 = \dfrac{{14\pi }}{3}\,\,\left( {c{m^3}} \right)\).
Vậy \({V_{\left( H \right)}} = {V_1} + {V_2} = 9\pi + \dfrac{{14}}{3}\pi = \dfrac{{41}}{3}\pi \,\,\left( {c{m^3}} \right)\).
Hướng dẫn giải:
+ Thể tích khối trụ chiều cao \(h\), bán kính đáy \(R\): \(V = \pi {R^2}h\).
+ Thể tích khối nón cụt chiều cao \(h\), hai bán kính đáy \(r;\,\,R\): \(V = \dfrac{1}{3}\pi \left( {{r^2} + rR + {R^2}} \right)h\).
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
