Một nguồn phát sóng cơ trên mặt nước đặt tại O, sóng có biên độ A, chu kì T, bước sóng λ. Hai điểm M, N cùng nằm trên một hướng truyền sóng cách nhau \(d = \frac{\lambda }{3}\), N gần nguồn hơn. Coi biên độ không đổi khi truyền đi. Tại thời điểm t1 = 0, M và N có li độ uM = + 3 cm và uN = - 3 cm. Ở thời điểm t2 liền sau đó, N có li độ uN = + A. Thời điểm t2 là:
Trả lời bởi giáo viên
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta có hình vẽ:
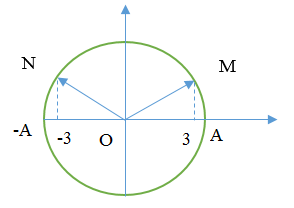
Vậy N đến vị trí có li độ A lần đầu tiên thì ON quét được một góc là:
\(\alpha = \frac{\pi }{6} + \pi = \frac{{7\pi }}{6}\)
Vậy thời gian để N có li độ A là:
\(t = \frac{\alpha }{{2\pi }}.T = \frac{7}{{12}}.T\)
Hướng dẫn giải:
Sử dụng VTLG.
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta biểu diễn được trên VTLG.

