Câu hỏi:
2 năm trước
Một miếng đất hình thang có diện tích là $864{m^2}$, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm $5m$ thì được miếng đất hình thang mới có diện tích bằng $924{m^2}$. Tìm độ dài mỗi đáy của miếng đất hình thang lúc chưa mở rộng.
Trả lời bởi giáo viên
Đáp án đúng:
B. Đáy lớn: \(42m\); đáy bé \(30m\)
Ta có hình vẽ như sau:
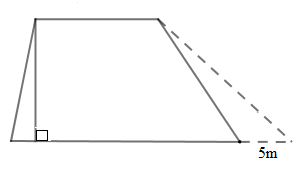
Sau khi mở rộng, diện tích miếng đất tăng thêm là:
$924 - 864 = 60\;({m^2})$
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
Chiều cao của miếng đất hình thang là:
\(60 \times 2:5 = 24\;(m)\)
Tổng độ dài hai đáy của hình thang là:
\(864 \times 2:24 = 72\;(m)\)
Độ dài đáy lớn của miếng đất đó là:
\((72 + 12):2 = 42\;(m)\)
Độ dài đáy bé của miếng đất đó là:
\(72 - 42 = 30\;(m)\)
Đáp số: đáy lớn: \(42m\); đáy bé: \(30m\).
Hướng dẫn giải:
- Tính diện tích phần đất tăng thêm.
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
- Tính chiều cao của hình thang ta lấy diện tích phần đất tăng thêm nhân với \(2\) rồi chia cho độ dài đáy \(5m\).
- Tính tổng độ dài hai đáy của hình thang ta lấy diện tích hình thang nhân với \(2\) rồi chia cho chiều cao.
- Giải bài toán tìm hai số khi biết tổng và hiệu để tìm độ dài mỗi đáy theo công thức:
Số lớn = (tổng + hiệu) \(:\,\,2\) ; Số bé = (tổng – hiệu) \(:\,\,2\)
Giải thích thêm:
- Học sinh có thể làm sai khi tính chiều cao bằng cách lấy diện tích phần đất tăng thêm chia cho \(5\).
- Học sinh có thể làm sai khi tính tổng độ dài hai đáy bằng cách lấy diện tích hình thang chia cho chiều cao.
Câu hỏi khác
Câu 3:
.jpg)
109
