Câu hỏi:
2 năm trước
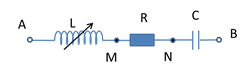
Một mạch điện gồm điện trở thuần $R$, tụ điện $C$ và cuộn cảm thuần $L$ mắc nối tiếp, trong đó độ tự cảm $L$ có thể thay đổi được. Đặt vào mạch điện một điện áp xoay chiều thì điện áp hiệu dụng trên mỗi phần tử lần lượt là $U_R = 40V$, $U_C = 60V$, $U_L=90V$. Giữ nguyên điện áp, thay đổi độ tự cảm $L$ để điện áp hiệu dụng giữa hai đầu cuộn cảm là $60V$ thì điện áp hiệu dụng giữa hai đầu điện trở gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: $U_R = 40V$; $U_C=60 V$; $U_L= 90V$
=> \(1,5{U_R} = {\text{ }}{U_C} \to 1,5R = {Z_C}\)
\( \to U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{40}^2} + {{\left( {90 - 60} \right)}^2}} = 50V\)
Thay đổi $L$ để \({U_L}' = {\text{ }}60V\)
Ta có: ${Z_C} = 1,5R \to {U_C}' = 1,5{U_R}'$, từ đó ta được:
\(\begin{array}{l}{50^2} = U{'}_R^2 + {\left( {{U_L}' - {U_C}'} \right)^2}\\ \leftrightarrow {50^2} = U{'}_R^2 + {\left( {60 - 1,5U{'_R}} \right)^2}\\ \to \left[ \begin{array}{l}{U_R}' = 48,39V\\{U_R}' = 6,99V\end{array} \right.\end{array}\)
Hướng dẫn giải:
Sử dụng công thức: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
