Câu hỏi:
2 năm trước
Một kính thiên văn khúc xạ được điều chỉnh cho một nguời có mắt bình thường nhìn được rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 62cm và số bội giác của kính là 30. Vật quan sát Mặt Trăng có góc trông \({\alpha _0} = \frac{1}{{100}}ra{\rm{d}}\). Đường kính của mặt trăng cho bởi vật kính là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có
+ Sơ đồ tạo ảnh qua hệ thấu kính:
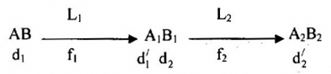
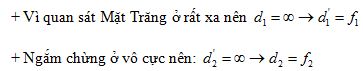
+ Khoảng cách giữa hai kính: \({O_1}{O_2} = {f_1} + {f_2} = 62cm\,\,\,\left( 1 \right)\)
+ Số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = 30\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta suy ra: \(\left\{ \begin{array}{l}{f_1} = 60cm\\{f_2} = 2cm\end{array} \right.\)
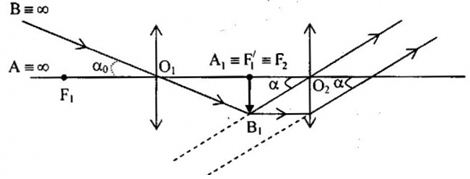
Ta có:
\(\begin{array}{l}\tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\\ \to {A_1}{B_1} = {f_1}\tan {\alpha _0} \approx {f_1}.{\alpha _0} = \frac{{60}}{{100}} = 0,6\left( {cm} \right)\end{array}\)
Hướng dẫn giải:
+ Vẽ sơ đồ tạo ảnh qua hệ thấu kính
+ Quan sát vật ở rất xa: \({d_1} = \infty \)
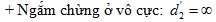
+ Sử dụng công thức tính khoảng cách giữa hai kính khi ngắm chừng ở vô cực: \({O_1}{O_2} = {f_1} + {f_2}\)
+ Sử dụng công thức tính số bội giác khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
+ Vẽ hình, sử dụng công thức: \(\tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\)
