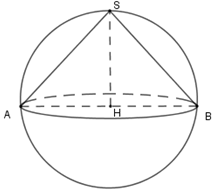
Một hình nón có đỉnh \(S\), đáy là đường tròn \(\left( C \right)\) tâm \(O\), bán kính \(R\) bằng với đường cao của hình nón. Tỉ số thể tích của hình nón và hình cầu ngoại tiếp hình nón bằng:

Cho hai đường thẳng: $\left(d_{1}\right): 3 x+2 y=a$ và $\left(d_{2}\right): x+b y=3.$ Biết rằng $\left(d_{1}\right)$ đi qua điểm $A(1 ; 1)$ và $\left(d_{2}\right)$ đi qua điểm $B(-5 ; 2)$. Khi đó giao điểm của hai đường thẳng $\left(d_{1}\right)$ và $\left(d_{2}\right)$ có tọa độ là:

Ba xạ thủ $A_{1}, A_{2}, A_{3}$ độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết xác suất bắn trúng mục tiêu của $A_{1}, A_{2}, A_{3}$ tương ứng là 0,$7 ; 0,6$ và $0,5$ . Tính xác suất để có ít nhất một xạ thủ bắn trúng

Quan sát biểu đồ và cho biết, khoảng thời gian nào không khí ô nhiễm nhất?

Hai đồ thị hàm số \(y =  - {x^2} - 2x + 3\) và \(y = {x^2} - m\) (với \(m\)  là tham số) có điểm chung khi và chỉ khi \(m\)  thỏa mãn: