Câu hỏi:
2 năm trước
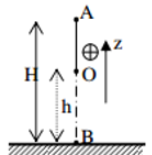
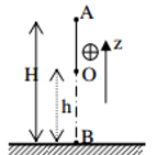
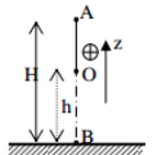
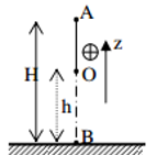
Một con lắc đơn dài \(2m\) treo vật \(m = 200g\). Kéo vật ra khỏi vị trí cân bằng sao cho phương sợi dây hợp với phương thẳng đứng một góc \({60^0}\) rồi thả nhẹ, bỏ qua ma sát, lấy \(g = 10m/{s^2}\). Vận tốc vật qua vị trí cân bằng là:
Trả lời bởi giáo viên
Đáp án đúng: a
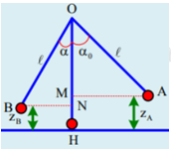
Chọn gốc thế năng tại H.
+ Cơ năng của vật tại H:
\({{\rm{W}}_H} = {{\rm{W}}_{tH}} + {{\rm{W}}_{dH}} = \dfrac{1}{2}mv_H^2\)
+ Cơ năng của vật tại B:
\({{\rm{W}}_B} = {{\rm{W}}_{tB}} + {{\rm{W}}_{dB}} = mg.{z_B} = mg.l.\left( {1 - \cos {\alpha _0}} \right)\)
Áp dụng định luật bảo toàn cơ năng tại H và B ta có:
\(\begin{array}{*{20}{l}}{{{\rm{W}}_H} = {{\rm{W}}_B} \Leftrightarrow \dfrac{1}{2}mv_{\max }^2 = mgl.\left( {1 - \cos {\alpha _0}} \right)}\\{\begin{array}{*{20}{l}}{ \Rightarrow {v_H} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} }\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\, = \sqrt {2.10.2.\left( {1 - \cos 60} \right)} = 4,47m/s}\end{array}}\end{array}\)
Hướng dẫn giải:
Cơ năng của vật chuyển động trong trọng trường :
\(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + mgz\)
Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn.
