Một chiếc cổng như hình vẽ, trong đó CD=6m,AD=4m, phía trên cổng có dạng hình parabol
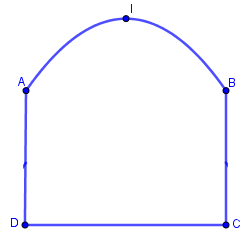
Người ta cần thiết kế cổng sao cho những chiến xe container chở hàng với bề ngang thùng xe là 4m, chiều cao là 5,2m có thể đi qua được (chiều cao được tính từ mặt đường đến nóc thùng xe và thùng xe có dạng hình hộp chữ nhật). Hỏi đỉnh I của parabol (theo mép dưới của cổng) cách mặt đất tối thiểu là bao nhiêu?
Chỉ điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
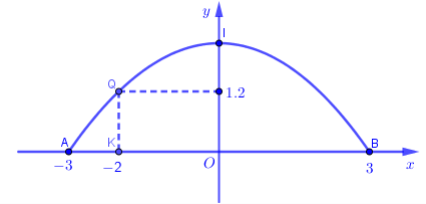
Gọi O là trung điểm của AB, K là điểm thuộc đoạn thẳng OA sao cho OK=2m. Chọn hệ tọa độ như hình vẽ. Khi đó phương trình của đường cong parabol có dạng y=ax2+c. Theo giả thiết ta có parabol đi qua (−2;1,2),(−3;0) nên ta có:
{4a+c=1,29a+c=0⇔{a=−625c=5425
⇒y=−625x2+5425
Vậy đỉnh I của parabol (theo mép dưới của cổng) cách mặt đất tối thiểu là h=5425+4=15425(m)
Hướng dẫn giải:
Bước 1: Gắn hệ trục tọa độ cho phần Parabol
Bước 2: Viết phương trình của Parabol
Bước 3: Tính chiều cao h của đỉnh I so với mặt đất.


