Câu hỏi:
2 năm trước
Một bản mặt song song có bề dày d = 10cm, chiết suất n = 1,5 đặt trong không khí. Chiếu tới bản một tia tới SI có góc tới 450. Khoảng cách giữa tia tới và tia ló:
Trả lời bởi giáo viên
Đáp án đúng: c
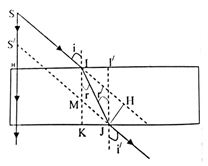
Theo định luật luật khúc xạ ánh sáng, ta có: \(1.\sin {45^0} = 1,5.{\mathop{\rm s}\nolimits} {\rm{inr}} \to {\mathop{\rm s}\nolimits} {\rm{inr}} = \dfrac{{\sqrt 2 }}{3} \to r = 28,{13^0}\)
- Tia tới và tia ló qua bản mặt song song luôn song song:
Từ hình, ta có:
\(IJ = \sqrt {I{K^2} + J{K^2}} \)
Lại có \(\left\{ \begin{array}{l}IK = d\\KJ = \tan r.IK = \tan r.d\end{array} \right.\)
Suy ra:
\(\begin{array}{l}IJ = \sqrt {I{K^2} + J{K^2}} = \sqrt {{d^2} + {{(d{\mathop{\rm t}\nolimits} {\rm{anr}})}^2}} \\ = \sqrt {{{10}^2} + {{\left( {10.\tan 28,{{13}^0}} \right)}^2}} = 11,34cm\end{array}\)
Xét tam giác IJH, có:
\(\sin \widehat {JIH} = \dfrac{{JH}}{{IJ}}\)
Lại có \(\widehat {JIH} = i - r\)
Ta suy ra: \(\sin \widehat {JIH} = \sin \left( {i - r} \right) = \dfrac{{JH}}{{IJ}}\)
\( \Rightarrow JH = IJsin(i - r) = 11,34.sin({45^0} - 28,{13^0}) \approx 3,3cm\)
Hướng dẫn giải:
+ Dựng ảnh qua bản mặt song song
+ Vận dụng biểu thức của định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
