Câu hỏi:
2 năm trước
Một bản hai mặt song song có bề dày \(6{\rm{ }}cm\), chiết suất \(n{\rm{ }} = {\rm{ }}1,5\) được đặt trong không khí. Điểm sáng \(S\) cách bản \(20{\rm{ }}cm\).
Ảnh \(S'\) của \(S\) qua bản hai mặt song song cách \(S\) một khoảng:
Trả lời bởi giáo viên
Đáp án đúng: b
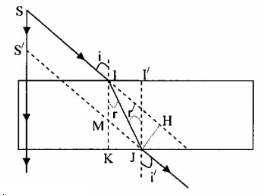
- Độ dời ảnh: SS’ = IM = IK – MK = e – MK
- Xét tam giác vuông MKJ: \(MK = \dfrac{{KJ}}{{\tan i}} = \dfrac{{II'}}{{\tan i}}\)
- Xét tam giác vuông II’J: \(II' = JI'.{\mathop{\rm t}\nolimits} {\rm{anr}} = e.{\mathop{\rm t}\nolimits} {\rm{anr}}\)
=> \(MK = \dfrac{{e.{\mathop{\rm t}\nolimits} {\rm{anr}}}}{{\tan i}}\)
=> \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\)
Với góc tới i nhỏ ta có: \(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\~e.(1 - \dfrac{{{\rm{Sin r}}}}{{Sini}}) = e.(1 - \dfrac{{{n_1}}}{{{n_2}}})\)
- Thay số: \(e = 6cm;{n_1} = 1;{n_2} = 1,5 \to SS' = 6.(1 - \dfrac{1}{{1,5}}) = 2cm\)
Hướng dẫn giải:
Sử dụng công thức độ dời ảnh quan bản mặt song song:
\(SS' = e.(1 - \dfrac{{{\rm{tan r}}}}{{\tan i}})\~e.(1 - \dfrac{{{\rm{Sin r}}}}{{Sini}}) = e.(1 - \dfrac{{{n_1}}}{{{n_2}}})\) với góc tới i nhỏ, e: bề dày của bản mặt song song
