Khối chóp có đáy là hình bình hành, một cạnh đáy bằng \(a\) và các cạnh bên đều bằng \(a\sqrt 2 \). Thể tích của khối chóp có giá trị lớn nhất là:

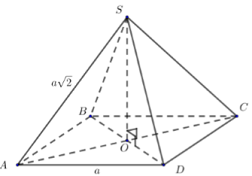
Gọi \(O = AC \cap BD\).

Tam giác \(SAC\) cân tại \(S\), \(SO\) là trung tuyến \( \Rightarrow SO \bot AC\).

Tam giác \(SBD\) cân tại \(S\), \(SO\) là trung tuyến \( \Rightarrow SO \bot BD\).

\( \Rightarrow SO \bot \left( {ABCD} \right)\).

Vì \(SA = SB = SC = SD\), \(SO \bot \left( {ABCD} \right)\) nên \(O\) là tâm đường tròn ngoại tiếp \(ABCD\).

Hình bình hành \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(ABCD\) phải là hình chữ nhật.

Theo bài ra ta giả sử \(AD = a\) và đặt \(AB = x\,\,\left( {x > 0} \right)\).

Áp dụng định lí Pytago trong tam giác vuông \(ABC\) có: \(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {x^2}} \).

\( \Rightarrow AO = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {{a^2} + {x^2}} \).

Áp dụng định lí Pytago trong tam giác vuông \(SOA\) có: \(SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {2{a^2} - \dfrac{{{a^2} + {x^2}}}{4}}  = \dfrac{1}{2}\sqrt {7{a^2} - {x^2}} \).

Khi đó ta có \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{1}{2}\sqrt {7{a^2} - {x^2}} .ax = \dfrac{a}{6}x\sqrt {7{a^2} - {x^2}} \).

Áp dụng BĐT Cô-si ta có: \(x\sqrt {7{a^2} - {x^2}}  \le \dfrac{{{x^2} + 7{a^2} - {x^2}}}{2} = \dfrac{{7{a^2}}}{2}\) \( \Rightarrow {V_{S.ABCD}} \le \dfrac{a}{6}.\dfrac{{7{a^2}}}{2} = \dfrac{{7{a^3}}}{{12}}\).

Dấu “=” xảy ra \( \Leftrightarrow {x^2} = 7{a^2} - {x^2} \Leftrightarrow x = \dfrac{{a\sqrt {14} }}{2}\).

Vậy thể tích khối chóp \(S.ABCD\) đạt giá trị lớn nhất bằng \(\dfrac{{7{a^3}}}{{12}}\) \( \Leftrightarrow x = \dfrac{{a\sqrt {14} }}{2}\).