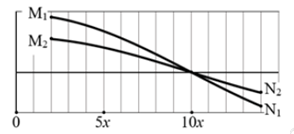
Hình vẽ bên mô phỏng một đoạn của một sợi dây đang có sóng dừng ổn định với bước sóng \(\lambda  = 50cm\) ở hai thời điểm khác nhau. Đường cong \({M_1}{N_1}\) là đoạn sợi dây ở thời điểm thứ nhất, đường cong \({M_2}{N_2}\) là đoạn dây đó ở thời điểm thứ hai. Biết tỉ lệ các khoảng cách \(\dfrac{{{M_1}{M_2}}}{{{N_1}{N_2}}} = \dfrac{8}{5}\) . Giá trị của \(x\) trên hình vẽ xấp xỉ là

Đề thi thử THPT chuyên Lam Sơn - 2021

Trong hệ sóng dừng trên một sợi dây, khoảng cách giữa hai bụng liên tiếp bằng

Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6 cm. Trên dây các phần tử sóng dao động với tần số 5 Hz và biên độ lớn nhất là 3 cm. Gọi N là vị trí của một nút sóng, C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5 cm và 7,0 cm. Tại thời điểm t₁ (s), phần tử C có li độ 1,5 cm và đang hướng về vị trí cân bằng. Vào thời điểm \({t_2} = {t_1} + \frac{{85}}{{40}}\,\,\left( s \right)\), phần tử D có li độ là

Trong giờ thực hành hiện tượng sóng dừng trên dây, một học sinh thực hiện như sau: tăng dần tần số của máy phát dao động thì thấy rằng khi sóng dừng xuất hiện trên dây tương ứng với \(1\) bó sóng và \(9\) bó sóng thì tần số thu được thỏa mãn \({f_9} - {f_1} = 200(Hz).\) Khi trên dây xuất hiện sóng dừng với \(6\) nút sóng thì máy phát tần số hiện giá trị là  

Trên một sợi dây đang có sóng dừng. Biết sóng truyền trên dây có bước sóng \(30 cm\). Khoảng cách ngắn nhất từ một nút đến một bụng là

Cho sợi dây AB dài đang dao động và trên dây có sóng dừng. Người ta đo được chu kỳ sóng là 12s. Hỏi khoảng thời gian hai lần liên tiếp sợi dây duỗi thẳng là bao nhiêu?

Trên một sợi dây đang có sóng dừng với bề rộng của một bụng sóng là \(3 cm\). Biên độ dao động của điểm bụng là  

Trên một sợi dây dài 2 m. Hai đầu cố định, đang có sóng dừng. Tốc độ truyền sóng trên dây là 20 m/s; tần số của sóng có giá trị trong khoảng từ 11 Hz đến 19 Hz. Nếu tính cả hai đầu dây thì số nút sóng trên dây là