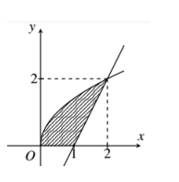
Hình phẳng D (phần gạch chéo trên hình) giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \sqrt {2x} \), đường thẳng \(d:\,\,y = ax + b\,\,\left( {a \ne 0} \right)\) và trục hoành. Tính thể tích khối tròn xoay thu được khi hình phẳng D quay quanh trục Ox.
Trả lời bởi giáo viên
Đường thẳng đi đi qua hai điểm \(\left( {1;0} \right);\,\,\left( {2;2} \right)\) nên có phương trình \(\dfrac{{x - 1}}{{2 - 1}} = \dfrac{{y - 0}}{{2 - 0}} \Leftrightarrow y = 2x - 2\)
Khi đó thể tích phần tròn xoay cần tính là:
\(\begin{array}{l}V = \pi \int\limits_0^1 {2xdx} + \pi \int\limits_1^2 {\left| {2x - {{\left( {2x - 2} \right)}^2}} \right|dx} \\V = \pi \int\limits_0^1 {2xdx} + \pi \int\limits_1^2 {\left| { - 4{x^2} + 10x - 4} \right|dx} \\V = \pi .\left. {{x^2}} \right|_0^1 + \left. {\pi \left( { - \dfrac{{4{x^3}}}{3} + 5{x^2} - 4x} \right)} \right|_1^2\\V = \pi \left( {1 + \dfrac{4}{3} + \dfrac{1}{3}} \right) = \dfrac{{8\pi }}{3}\end{array}\).
Hướng dẫn giải:
Sử dụng công thức ứng dụng tích phân tính thể tích khối tròn xoay.
Câu hỏi khác
(Nguồn: ourwordindata.org)- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
