Câu hỏi:
2 năm trước
Hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh $a$ và diện tích hình chữ nhật \(A{\rm{D}}C'B'\) bằng \(2{{\rm{a}}^2}\), diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
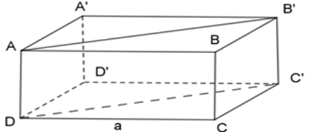
Ta có \(A{\rm{D}}C'B'\) là hình chữ nhật.
\( \Rightarrow {S_{A{\rm{D}}C'B'}} = A{\rm{D}}.DC' = 2{{\rm{a}}^2} \Rightarrow a.DC' = 2{{\rm{a}}^2} \Rightarrow DC' = 2{\rm{a}}\)
Xét tam giác vuông \(CC'D\) ta có:
\(CC{'^2} + C{{\rm{D}}^2} = C'{D^2} \Leftrightarrow CC{'^2} + {a^2} = {(2{\rm{a}})^2} \Leftrightarrow CC{'^2} = 4{{\rm{a}}^2} - {a^2} = 3{{\rm{a}}^2} \Rightarrow CC' = a\sqrt 3 \)
Vậy diện tích xung quanh của hình hộp chữ nhật là:
Sxq \( = 2.p.CC' = 2.\dfrac{{4{\rm{a}}}}{2}.a\sqrt 3 = 4{{\rm{a}}^2}\sqrt 3 \)
Hướng dẫn giải:
- Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật \({S_{xq}} = 2ph\) (với p là nửa chu vi đáy) và công thức tính diện tích hình chữ nhật, định lý Pytago
