Trả lời bởi giáo viên
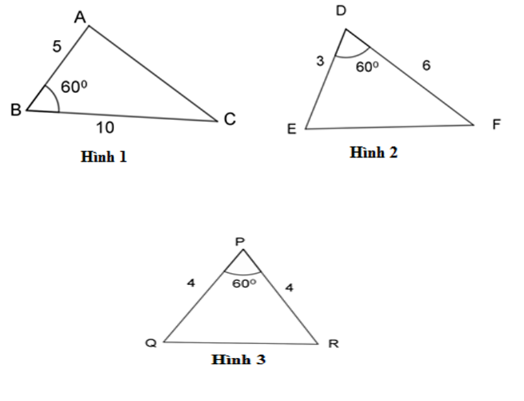
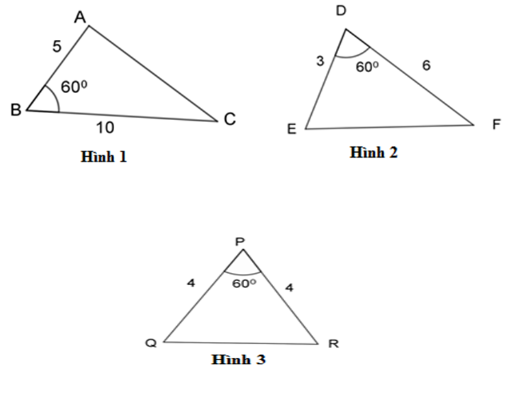
Có: \(\dfrac{{BA}}{{BC}} = \dfrac{5}{{10}} = \dfrac{1}{2},\;\dfrac{{DE}}{{DF}} = \dfrac{3}{6} = \dfrac{1}{2},\;\dfrac{{PQ}}{{PR}} = \dfrac{4}{4} = 1 \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}} = \dfrac{1}{2}.\)
Xét \(\Delta ABC\) và $\Delta EDF$ ta có:
$\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}\,\,\left( {cmt} \right) $$\Leftrightarrow \dfrac{{DE}}{{BA}} = \dfrac{{DF}}{{BC}}$
$\widehat B = \widehat D = {60^0}\;(gt)$
$\Rightarrow \Delta ABC\backsim \Delta EDF\,\,\,\left( {c - g - c} \right).$
Hướng dẫn giải:
Bước 1: Xét tỉ số độ dài của các cặp cạnh từng tam giác.
Bước 2: Thấy cặp tam giác nào có tỉ số cặp cạnh của từng tam giác bằng nhau và góc xen giữa cặp cạnh đó bằng nhau thì cặp cạnh đang xét đồng dạng với nhau theo trường hợp cạnh – góc – cạnh.
Giải thích thêm:
- Học sinh cần xác định đúng chứng minh cặp tam giác đồng dạng theo trường hợp nào để tìm ra kết quả tối ưu nhất.
- Học sinh cần viết các cặp đoạn thẳng tỉ lệ và cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.