Câu hỏi:
2 năm trước
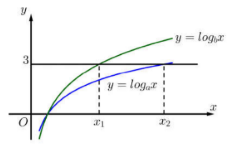
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
Dựa vào đồ thị hàm số ta thấy \({x_1}\) là nghiệm của phương trình hoành độ giao điểm \({\log _b}{x_1} = 3 \Leftrightarrow {x_1} = {b^3}.\)
Và \({x_2}\) là nghiệm của phương trình hoành độ giao điểm \({\log _a}{x_2} = 3 \Leftrightarrow {x_2} = {a^3}.\)
Theo đề bài ta có: \({x_2} = 2{x_1} \Rightarrow {a^3} = 2{b^3} \Leftrightarrow \dfrac{{{a^3}}}{{{b^3}}} = 2 \Leftrightarrow \dfrac{a}{b} = \sqrt[3]{2}.\)
Hướng dẫn giải:
Dựa vào đồ thị hàm số, xác định các giá trị của \({x_1},\,{x_2}\) theo \(a\) và \(b.\) Từ đó tính giá trị của \(\dfrac{a}{b}.\)
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 đề số 2 Toán 12 có lời giải chi tiết
