Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) có bảng biến thiên:

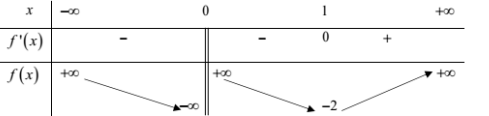
Tìm số nghiệm của phương trình \(2f\left( {3x - 5} \right) - 7 = 0\)

Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b

Đáp án:

Cho phương trình: \({x^2} - 2mx + 2m - 4 = 0\). Có bao nhiêu giá trị nguyên của m nhỏ hơn 2020 để phương trình có 2 nghiệm dương phân biệt

Cho đường cong \(\left( {{C_m}} \right):{x^2} + {y^2}  - 8x + 6y + 3m = 0\). Với giá trị nào của tham số thực \(m\) thì \(\left( {{C_m}} \right)\) là phương trình đường tròn với bán kính đường tròn bằng 4?

Biểu đồ dưới đây biểu thị dân số của Nhật Bản năm 2016.

Nhóm tuổi nào có số dân đông nhất?

Điền số nguyên hoặc phân số dạng a/b vào chỗ trống

Cho hình chóp S.ABCD có đáy \({\rm{ABCD}}\) là hình vuông cạnh \({\rm{a}},{\rm{SA}}\) vuông góc với mặt phẳng \(({\rm{ABCD}})\) và \({\rm{SA}} = {\rm{a}}\). Gọi \({\rm{E}}\) là trung điểm của cạnh \({\rm{CD}}\). Tính theo a khoảng cách từ điểm \(S\) đến đường thẳng \({\rm{BE}}\)

Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh \(a\sqrt 2 ,SA\) vuông góc với mặt phẳng đáy, \(SA = a\sqrt 3 \). Góc giữa hai mặt phẳng \((SBD)\) và \((ABCD)\) bằng: