Câu hỏi:
2 năm trước
Hai điện tích q1 = 8. 10-8 C, q2 = -8. 10-8 C đặt tại A và B trong không khí biết AB = 4 cm. Tìm vectơ cường độ điện trường tại C trên đường trung trực của AB và cách AB 2 cm?
Trả lời bởi giáo viên
Đáp án đúng: c
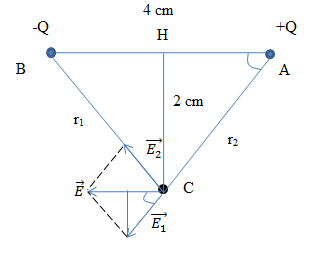
- Ta có: r1 = r2 = \(r = \sqrt {A{H^2} + A{C^2}} = 2\sqrt 2 \) cm Vì |q1| = |q2| và r1 = r2 => E1 = E2
- Từ hình vẽ ta có: \(E = 2{E_1}c{\rm{os}}\alpha \)
Với
\(\cos \alpha = \frac{{AH}}{{AC}} = \frac{2}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) => \(E = 2{E_1}\frac{{\sqrt 2 }}{2} = {E_1}\sqrt 2 \)
Ta có:
\({E_1} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\frac{{\left| {{{8.10}^{ - 8}}} \right|}}{{1.{{(2.\sqrt 2 {{.10}^{ - 2}})}^2}}} = {9.10^5}V/m\)
=> E ≈ 12,73. 105 V/m.
Hướng dẫn giải:
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
