Hai điểm sáng dao động điều hòa với cùng biên độ trên một đường thẳng, quanh vị trí cân bằng O. Các pha của hai dao động ở thời điểm t là a1 và a2 . Hình bên là đồ thị biểu diễn sự phụ thuộc của a1 và của a2 theo thời gian t. Tính từ t=0, thời điểm hai điểm sáng gặp nhau lần đầu là
Trả lời bởi giáo viên
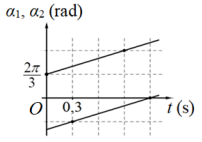
Vì đồ thị của α1, α2 theo t có dạng hai đường thẳng nên chúng có dạng.
+ α1 = ω1t + φ1
Tại thời điểm t = 0, α1 = φ1 = 2π/3
Tại thời điểm t = 0,9s; α1 = ω1.0,9+ φ1 = 4π/3 Vậy ω1 = 20π/27 rad/s
+ α2 = ω2t + φ2
Tại thời điểm t = 0,3s: α2 = 0,3.ω2 + φ2= -2π/3
Tại thời điểm t = 1,2s : α2 = 1,2.ω2 + φ2= 0
Giải hai phương trình bậc nhất ta được ω2 = 20π/27 rad/s và φ2 = 8π/9
+ Vậy hai dao động có pha là (20π27t+2π3) và (20π27t+8π9)
Để hai điểm sáng gặp nhau thì Acos(20π27t+2π3) = Acos (20π27t+8π9)
Ta có :
(20π27t+2π3)=±(20π27t+8π9)+2kπ⇒(20π27t+2π3)=−(20π27t+8π9)+2kπ⇒40π27t=−8π9−2π3+2kπ
Hai điểm sáng gặp nhau ứng với giá trị k nhỏ nhất để t dương
Vậy tmin = 0,15s
Hướng dẫn giải:
- Đồ thị hàm bậc nhất theo thời gian có dạng đường thẳng.
- Hai vật gặp nhau khi chúng có li độ bằng nhau

