Hai điểm \(A\) và \(B\) trên mặt nước cách nhau \(12cm\) phát ra hai sóng kết hợp có phương trình: \({u_1} = {u_2} = acos40\pi t\left( {cm} \right)\),tốc độ truyền sóng trên mặt nước là \(30cm/s\). Xét đoạn thẳng \(CD{\rm{ }} = {\rm{ }}6cm\) trên mặt nước có chung đường trung trực với \(AB\). Khoảng cách lớn nhất từ \(CD\) đến \(AB\) sao cho trên đoạn \(CD\) chỉ có \(5\) điểm dao động với biên độ cực đại là
Trả lời bởi giáo viên
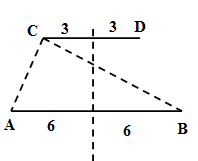
Ta có:
+ Tần số của sóng : \(f = \frac{\omega }{{2\pi }} = \frac{{40\pi }}{{2\pi }} = 20Hz\)
+ Bước sóng : \(\lambda = \frac{v}{f} = \frac{{30}}{{20}} = 1,5cm\)
Để trên \(CD\) xa \(AB\) nhất mà trên đoạn \(CD\) chỉ có \(5\) điểm dao động cực đại thì \(C\) và \(D\) nằm trên các đường cực đại bậc \(2\)
\(\begin{array}{l}CA - CB = - 2\lambda \\ \Leftrightarrow \sqrt {{d^2} + {3^2}} - \sqrt {{d^2} + {9^2}} = - 2.1,5\\ \to d = 10,06cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính tần số: \(f = \frac{\omega }{{2\pi }}\)
+ Sử dụng lí thuyết về giao thoa hai nguồn cùng pha
+ Sử dụng điều kiện để điểm dao động với biên độ cực đại trong giao thoa hai nguồn cùng pha là \({d_2} - {d_1} = k\lambda \)

