Gọi a, b lần lượt là số điểm cực đại và số điểm cực tiểu của hàm số \(y = \left( {{x^3} + 3x + 1} \right){e^{ - 2x}}\). Tính \(2a - b\).
Trả lời bởi giáo viên
Ta có \(y = \left( {{x^3} + 3x + 1} \right){e^{ - 2x}}\). Tập xác định: \(D = \mathbb{R}\).
\({y^\prime } = {\left( {{x^3} + 3x + 1} \right)^\prime }{e^{ - 2x}} + \left( {{x^3} + 3x + 1} \right){\left( {{e^{ - 2x}}} \right)^\prime } = \left( {3{x^2} + 3} \right){e^{ - 2x}} - 2{{\rm{e}}^{ - 2x}}\left( {{x^3} + 3x + 1} \right).\)
\( = {e^{ - 2x}}\left( { - 2{x^3} + 3{x^2} - 6x + 1} \right);{y^\prime } = 0\) có một nghiệm là \({x_0}\).
Bảng biến thiên:
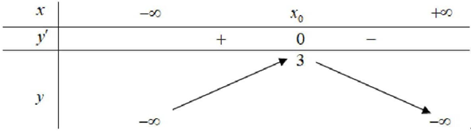
Suy ra hàm số có 1 điểm cực đại và 0 điểm cực tiểu.
Vậy \(2a - b = 2\).
Hướng dẫn giải:
- Giải phương trình \(y' = 0\) và lập bảng biến thiên
- Quan sát bảng biến thiên và kết luận số cự trị.


