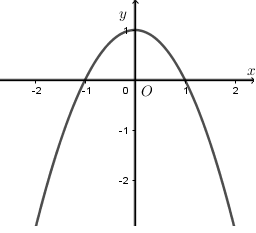
Diện tích hình phẳng giới hạn bởi nửa đường tròn ${x^2} + {y^2} = 2,y > 0$ và parabol $y = {x^2}$ bằng:
Trả lời bởi giáo viên
${x^2} + {y^2} = 2(y > 0) \Leftrightarrow y = \sqrt {2 - {x^2}} $
+ Hoành độ giao điểm của 2 đường là nghiệm của phương trình:
$\sqrt {2 - {x^2}} = {x^2} \Leftrightarrow {x^4} + {x^2} - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = - 2(L)\end{array} \right. \\\Leftrightarrow x = \pm 1$
+ Với \( - 1 \le x \le 1\) thì
\(\begin{array}{l} {x^2} \le 1 \Rightarrow {x^4} \le 1\\ \Rightarrow {x^4} + {x^2} - 2 = \left( {{x^4} - 1} \right) + \left( {{x^2} - 1} \right) \le 0\end{array}\)
\(\begin{array}{l} \Rightarrow 0 \le {x^4} \le 2 - {x^2}\\ \Rightarrow {x^2} \le \sqrt {2 - {x^2}} \end{array}\)
\( \Rightarrow {x^2} - \sqrt {2-{x^2}} \le 0 \Rightarrow \left| {\sqrt {2 - {x^2}} - {x^2}} \right| = \sqrt {2 - {x^2}} - {x^2}\)
+ Diện tích hình phẳng là:
$S = \int\limits_{ - 1}^1 {\left| {\sqrt {2 - {x^2}} - {x^2}} \right|dx} = \int\limits_{ - 1}^1 {\left( {\sqrt {2 - {x^2}} - {x^2}} \right)dx} = \int\limits_{ - 1}^1 {\sqrt {2 - {x^2}} dx} - \int\limits_{ - 1}^1 {{x^2}dx} $
+ Với ${I_1} = \int\limits_{ - 1}^1 {\sqrt {2 - {x^2}} dx} $
Đặt $x = \sqrt 2 \sin u \Rightarrow dx = \sqrt 2 \cos udu$
Khi $ x = -1 \Rightarrow u = - \dfrac{\pi }{4}$
$ x = 1 \Rightarrow u = \dfrac{\pi }{4}$
Do đó ${I_1} = \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {\sqrt {2 - 2{{\sin }^2}u} .\sqrt 2 \cos udu} = \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {2{{\cos }^2}udu} $$ = \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {(1 + \cos 2u)du} $
$ = \left. u \right|_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} + \left. {\dfrac{1}{2}\sin 2u} \right|_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} = \dfrac{\pi }{4} + \dfrac{\pi }{4} + \dfrac{1}{2}\sin \dfrac{\pi }{2} - \dfrac{1}{2}\sin \left( { - \dfrac{\pi }{2}} \right) = \dfrac{\pi }{2} + 1$
+ Với ${I_2} = \int\limits_{ - 1}^1 {{x^2}dx} = \dfrac{1}{3}\left. {{x^3}} \right|_{ - 1}^1 = \dfrac{1}{3} + \dfrac{1}{3} = \dfrac{2}{3}$
$ \Rightarrow S = {I_1} - {I_2} = \dfrac{\pi }{2} + 1 - \dfrac{2}{3} = \dfrac{\pi }{2} + \dfrac{1}{3}$
Hướng dẫn giải:
- Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\)
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)