Điền số thích hợp vào ô trống:
Một ô tô du lịch khởi hành từ A lúc \(5\) giờ \(40\) phút để đi về B. Cùng lúc đó một ô tô chở hàng đi từ B về A. Hai ô tô gặp nhau lúc \(8\) giờ \(30\) phút. Quãng đường AB dài \(306km\) và vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng.
Vậy vận tốc của ô tô du lịch là
km/giờ, vận tốc của ô tô chở hàng là
km/giờ.
Trả lời bởi giáo viên
Một ô tô du lịch khởi hành từ A lúc \(5\) giờ \(40\) phút để đi về B. Cùng lúc đó một ô tô chở hàng đi từ B về A. Hai ô tô gặp nhau lúc \(8\) giờ \(30\) phút. Quãng đường AB dài \(306km\) và vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng.
Vậy vận tốc của ô tô du lịch là
km/giờ, vận tốc của ô tô chở hàng là
km/giờ.
Ta có sơ đồ chuyển động của hai xe:
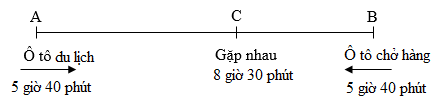
Thời gian đi để hai xe gặp nhau là:
$8$ giờ \(30\) phút $ - \,5$ giờ \(40\) phút $ = 2$ giờ \(50\) phút
Đổi $2$ giờ $50$ phút \( = \,2\dfrac{5}{6}\) giờ\( = \,\dfrac{{17}}{6}\) giờ
Tổng vận tốc của hai xe là:
\(306:\dfrac{{17}}{6} = 108\)(km/giờ)
Ta có sơ đồ:
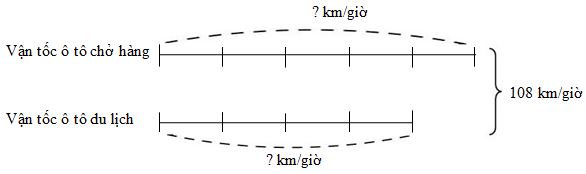
Theo sơ đồ, tổng số phần bằng nhau là:
\(5 + 4 = 9\) (phần)
Vận tốc ô tô chở hàng là:
\(108:9 \times 5 = 60\) (km/giờ)
Vận tốc ô tô du lịch là:
\(108 - 60 = 48\) (km/giờ)
Đáp số: Ô tô du lịch: \(48\) km/giờ;
Ô tô chở hàng: \(60\) km/giờ.
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là \(48\,;\,\,60\).
Hướng dẫn giải:
Theo đề bài, hai xe xuất phát cùng lúc. Để giải bài này ta làm như sau:
- Tính thời gian đi để gặp nhau ta lấy thời gian lúc gặp nhau trừ đi thời gian lúc hai ô tô xuất phát: $8$ giờ \(30\) phút $ - \,5$ giờ \(40\) phút và đổi kết quả vừa tìm được sang dạng số thập phân hoặc phân số có đơn vị là giờ.
- Tính tổng vận tốc hai xe ta lấy quãng đường AB chia cho thời gian đi để gặp nhau.
- Giải bài toán tìm hai số khi biết tổng và tỉ số của hai số. Theo đề bài, vận tốc ô tô du lịch bằng \(\dfrac{4}{5}\) vận tốc ô tô chở hàng nên ta vẽ sơ đồ biểu thị vận tốc ô tô du lịch gồm \(4\) phần bằng nhau, vận tốc ô tô chở hàng gồm 5 phần như thế. Để tìm hai số ta áp dụng công thức sau:
Số bé \(=\) (tổng : tổng số phần bằng nhau) \( \times \) số phần của số bé;
Số lớn \(=\) (tổng : tổng số phần bằng nhau) \( \times \) số phần của số lớn.
Giải thích thêm:
Học sinh cần chú ý tính đúng thời gian đi để gặp nhau, từ đó mới tính đúng tổng vận tốc của hai ô tô.