Điền số thích hợp vào ô trống:

Cho hình vẽ như sau:

 

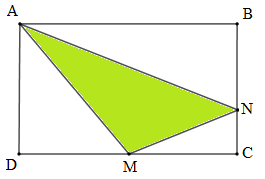
Biết  hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\)  (như hình vẽ). 

Diện tích tam giác $AMN$ là 

 \(cm^2\).

Theo đề bài:

\(\begin{array}{l}MC{\rm{ }} = {\rm{ }}MD \Rightarrow MC = MD = \dfrac{1}{2}DC\\BN = \dfrac{2}{3}BC \Rightarrow NC = \dfrac{1}{3}BC\end{array}\)

Ta có:

+) \({S_{ADM}} = \dfrac{1}{2} \times AD \times DM = \dfrac{1}{2} \times AD \times \dfrac{{DC}}{2} = \dfrac{1}{4} \times AD \times DC\)

 Suy ra diện tích tam giác \(ADM\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật $ABCD$.

Diện tích tam giác \(ADM\) là:

            \(96:4 = 24\;(c{m^2})\)

+) \({S_{ABN}} = \dfrac{1}{2} \times AB \times BN = \dfrac{1}{2} \times AB \times \dfrac{2}{3}BC = \dfrac{1}{3} \times AB \times BC\)

Suy ra diện tích tam giác \(ABN\) bằng \(\dfrac{1}{3}\) diện tích hình chữ nhật $ABCD$.

Diện tích tam giác \(ABN\) là:

            \(96:3 = 32\;(c{m^2})\)

+) \({S_{MNC}} = \dfrac{1}{2} \times MC \times NC = \dfrac{1}{2} \times \dfrac{1}{2}DC \times \dfrac{1}{3}BC = \dfrac{1}{{12}} \times DC \times BC\)

Suy ra diện tích tam giác \(MNC\) bằng \(\dfrac{1}{{12}}\) diện tích hình chữ nhật $ABCD$.

Diện tích tam giác \(MNC\)là:

            \(96:12 = 8\;(c{m^2})\)

Diện tích tam giác \(AMN\)là:

            \(96 - (24 + 32 + 8) = 32\;(c{m^2})\)

                                           Đáp số: \(32c{m^2}\).

Vậy đáp án đúng điền vào ô trống là \(32\).