Đề thi THPT QG - 2021 - mã 101
Xét các số phức \(z,\,{\rm{w}}\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {\rm{w}} \right| = 2.\) Khi \(\left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng?
Trả lời bởi giáo viên
Cách 1: Dùng phương pháp hình học \( \to \) Kỹ năng dồn số phức.
* \(P = \left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right| = \left| {\left( {z - 6 - 8i} \right) - \left( { - i\overline w } \right)} \right| = \left| {u - v} \right|\).
Trong đó: \(\left\{ \begin{array}{l}u = z - 6 - 8i\\v = - i\overline w \end{array} \right.\), \(u\) có điểm biểu diễn là \(A\), \(v\) có điểm biểu diễn là \(B\).
\( \Rightarrow P = \left| {u - v} \right| = AB \Rightarrow \) Cần đạt Min.
* \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z - 6 - 8i} \right) + 6 + 8i} \right| = 1 \Leftrightarrow \left| {u + 6 + 8i} \right| = 1\).
\( \Rightarrow \) Tập hợp điểm \(A\) biểu diễn số phức \(u\) là đường tròn: \(\left( {{C_1}} \right)\): \(\left\{ \begin{array}{l}I\left( { - 6; - 8} \right)\\{R_1} = 1\end{array} \right.\).
* \(\left| w \right| = 2 \Leftrightarrow \left| {\overline w } \right| = 2 \Leftrightarrow \left| { - i} \right|.\left| {\overline w } \right| = \left| { - i} \right|.2\) \( \Rightarrow \left| { - i\overline w } \right| = 2 \Leftrightarrow \left| v \right| = 2\).
\( \Rightarrow \) Tập hợp điểm \(B\) biểu diễn số phức \(v\) là đường tròn \(\left( {{C_2}} \right):\,\,\left\{ \begin{array}{l}O\left( {0;0} \right)\\{R_2} = 2\end{array} \right.\).
Có \(\left\{ \begin{array}{l}IA = {R_1} = 1\\OB = {R_2} = 2\\OI = 10\end{array} \right.\)
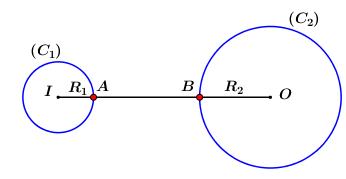
\( \Rightarrow A{B_{\min }} = IO - {R_1} - {R_2} = 10 - 1 - 2 = 7\).
Min đạt được khi: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \dfrac{9}{{10}}\overrightarrow {OI} \Rightarrow A\left( {\dfrac{{ - 27}}{5};\dfrac{{ - 36}}{5}} \right) \Rightarrow u = - \dfrac{{27}}{5} - \dfrac{{36}}{5}i\\\overrightarrow {OB} = \dfrac{1}{5}\overrightarrow {OI} \Rightarrow B\left( {\dfrac{{ - 6}}{5};\dfrac{{ - 8}}{5}} \right) \Rightarrow v = - \dfrac{6}{5} - \dfrac{8}{5}i\end{array} \right.\).
\( \Rightarrow \left\{ \begin{array}{l}z = u + 6 + 8i = \dfrac{3}{5} + \dfrac{4}{5}i\\ - i\overline w = v \Rightarrow \overline w = \dfrac{v}{{ - i}} = \dfrac{{ - \dfrac{6}{5} - \dfrac{8}{5}i}}{{ - i}} = \dfrac{8}{5} - \dfrac{6}{5}i \Rightarrow w = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
\( \Rightarrow \left| {z - w} \right| = \left| {\left( {\dfrac{3}{5} + \dfrac{4}{5}i} \right) - \left( {\dfrac{8}{5} + \dfrac{6}{5}i} \right)} \right| = \dfrac{{\sqrt {29} }}{5}\).
Cách 2: Phương pháp dùng BĐT vectơ
Ta có BĐT cho 3 vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) thì \(\left| {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right| \ge \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| - \left| {\overrightarrow c } \right|\).
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|\\\overrightarrow a = k\overrightarrow b \\\overrightarrow a = m\overrightarrow c \end{array} \right.\,\,\left( {k;m < 0} \right)\).
* Đặt \(P = \left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right| = \left| {\underbrace {\left( { - 6 - 8i} \right)}_{ = \overrightarrow a } + \underbrace z_{ = \overrightarrow b } + \underbrace {i\overline w }_{ = \overrightarrow c }} \right|\)
Đặt \(\left\{ \begin{array}{l}\left( { - 6 - 8i} \right) \Leftrightarrow \overrightarrow a \left( { - 6; - 8} \right) \Rightarrow \left| {\overrightarrow a } \right| = 10\\z \Leftrightarrow \overrightarrow b \Rightarrow \left| {\overrightarrow b } \right| = 1\\i\overline w \Leftrightarrow \overrightarrow c \Rightarrow \left| {\overrightarrow c } \right| = \left| {i\overline w } \right| = \left| w \right| = 2\end{array} \right.\).
\( \Rightarrow P = \left| {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right| \ge \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| - \left| {\overrightarrow c } \right| = 10 - 1 - 2 = 7\).
\( \Rightarrow {P_{\min }} = 7\), đạt Min khi \(\left\{ \begin{array}{l}\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|\,\,\left( {dung\,\,do\,\,10 > 1 + 2} \right)\\\overrightarrow a = - 10\overrightarrow b \Leftrightarrow \overrightarrow b = - \dfrac{1}{{10}}\overrightarrow a = \left( {\dfrac{3}{5};\dfrac{4}{5}} \right)\\\overrightarrow a = - 5\overrightarrow c \Leftrightarrow \overrightarrow c = - \dfrac{1}{5}\overrightarrow a = \left( {\dfrac{6}{5};\dfrac{8}{5}} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}z = \dfrac{3}{5} + \dfrac{4}{5}i\\i\overline w = \dfrac{6}{5} + \dfrac{8}{5}i \Leftrightarrow w = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
\( \Rightarrow \left| {z - w} \right| = \left| {\left( {\dfrac{3}{5} + \dfrac{4}{5}i} \right) - \left( {\dfrac{8}{5} + \dfrac{6}{5}i} \right)} \right| = \dfrac{{\sqrt {29} }}{5}\).
Hướng dẫn giải:
+) Dùng phương pháp hình học \( \to \) Kỹ năng dồn số phức.
* \(P = \left| {z + i\,\overline w - 6 - 8i} \right| = \left| {\left( {z - 6 - 8i} \right) - \left( { - i\overline w } \right)} \right| = \left| {u - v} \right|\).
Trong đó: \(\left\{ \begin{array}{l}u = z - 6 - 8i\\v = - i\overline w \end{array} \right.\), \(u\) có điểm biểu diễn là \(A\), \(v\) có điểm biểu diễn là \(B\).
+) Tìm tập hợp điểm biểu diễn số phức $u$ và $v$.
+) Tìm \(AB_\min\)

