Câu hỏi:
2 năm trước
Đề thi THPT QG - 2021 - mã 101
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\),\(AB = 2a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(C\)đến mặt phẳng \((SAB)\)bằng
Trả lời bởi giáo viên
Đáp án đúng: b
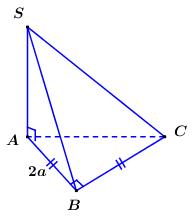
Nhận thấy \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,\,\left( {do\,\,SA \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\).
\( \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = BC\).
Mà \(\Delta ABC\) là tam giác vuông cân tại \(B\) \( \Rightarrow BC = AB = 2a\).
\( \Rightarrow d\left( {C;\left( {SAB} \right)} \right) = 2a\).
Hướng dẫn giải:
- Chứng minh \(BC \bot \left( {SAB} \right)\).
- Sử dụng tính chất tam giác vuông cân để tính khoảng cách.

