Câu hỏi:
2 năm trước
Đề thi THPT QG – 2021 lần 1– mã 104
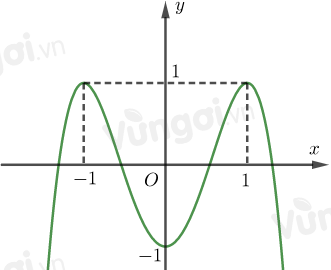
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong trong hình trên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\,\,\,\left( {a < - 1} \right)\\f\left( x \right) = b\,\,\,\left( { - 1 < b < 0} \right)\\f\left( x \right) = c\,\,\,\left( {0 < c < 1} \right)\\f\left( x \right) = d\,\,\,\left( {d > 1} \right)\end{array} \right.\)
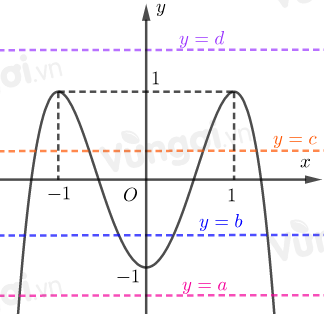
Dựa vào đồ thị ta thấy:
\(f\left( x \right) = a\) với \(a < - 1\) có \(2\) nghiệm.
\(f\left( x \right) = b\,\,\left( { - 1 < b < 0} \right)\) có \(4\) nghiệm.
\(f\left( x \right) = c\) với \(0 < c < 1\) có \(4\) nghiệm.
\(f\left( x \right) = d\) với \(d > 1\) vô nghiệm.
Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là \(10.\)
Hướng dẫn giải:
Tìm nghiệm của phương trình \(f\left( t \right) = 0\) \(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}t = {t_1}\\t = {t_2}\\...\end{array} \right.\\\end{array}\)
Tìm nghiệm của phương trình \(\left[ \begin{array}{l}f\left( x \right) = {t_1}\\f\left( x \right) = {t_2}\\...\end{array} \right.\)
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
