Câu hỏi:
2 năm trước
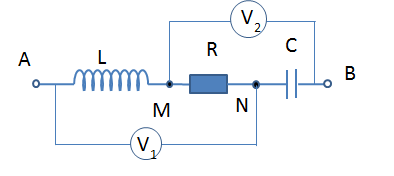
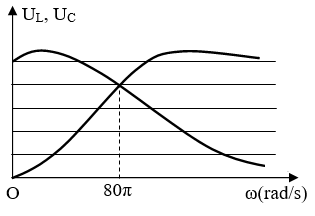
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi nhưng tần số góc \(\omega \) thay đổi được vào hai đầu đoạn mạch AB gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C mắc nối tiếp. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L là \({U_L}\) và điện áp hiệu dụng trên C là \({U_C}\) theo giá trị tần số góc \(\omega \). Khi điện áp hiệu dụng trên đoạn mạch chỉ chứa R và L là \({U_{RL}}\) đạt cực đại thì tần số góc \(\omega \) có giá trị là
Trả lời bởi giáo viên
Đáp án đúng: b
Từ đồ thị ta có khi \({\omega _0} = 80\pi \left( {rad/s} \right)\) thì \({U_L} = {U_C}\)
Đây cũng chính là giá trị tần số góc để mạch xảy ra cộng hưởng.
\({U_{RL}} = I.{Z_{RL}} = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\sqrt {{R^2} + Z_L^2} = \frac{U}{{\sqrt {1 + \frac{{ - 2\frac{L}{C} + \frac{1}{{{\omega ^2}{C^2}}}}}{{{R^2} + {{\left( {\omega L} \right)}^2}}}} }}\)
Xét hàm số: \(y = 1 + \frac{{ - \frac{{2L}}{C} + \frac{1}{{{\omega ^2}{C^2}}}}}{{{R^2} + {{\left( {\omega L} \right)}^2}}}\)
\({\left( {{U_{RL}}} \right)_{\max }}\) khi \({y_{\min }}\)
Ta có: \(y' = \frac{{\frac{{ - 2}}{{{\omega ^3}{C^2}}}\left( {{R^2} + {\omega ^2}{L^2}} \right) - 2\omega {L^2}\left( { - \frac{{2L}}{C} + \frac{1}{{{\omega ^2}{C^2}}}} \right)}}{{{{\left( {{R^2} + {\omega ^2}{L^2}} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow - \frac{2}{{{\omega ^3}{C^2}}}\left( {{R^2} + {\omega ^2}{L^2}} \right) - 2\omega {L^2}\left( { - \frac{{2L}}{C} + \frac{1}{{{\omega ^2}{C^2}}}} \right) = 0\)
\(\begin{array}{l} \Leftrightarrow {R^2} + {\omega ^2}{L^2} + {\omega ^4}{L^2}{C^2}\left( { - \frac{{2L}}{C} + \frac{1}{{{\omega ^2}{C^2}}}} \right) = 0\\ \Leftrightarrow - 2{L^3}C{\omega ^4} + 2{L^2}{\omega ^2} + {R^2} = 0\end{array}\)
\( \Rightarrow \left\{ \begin{array}{l}{\omega ^2} > 0\\{\omega ^2} = - \frac{b}{{2a}} = - \frac{{2{L^2}}}{{2.\left( { - 2{L^3}C} \right)}} = \frac{1}{{2LC}} = \frac{{\omega _0^2}}{2}\end{array} \right.\)
\( \Rightarrow \omega = \frac{{{\omega _0}}}{{\sqrt 2 }} = \frac{{80\pi }}{{\sqrt 2 }} = 177,71{\rm{r}}a{\rm{d}}/s\)
Hướng dẫn giải:
+ Đọc đồ thị điện áp
+ Sử dụng biểu thức: \({U_{RL}} = I.{Z_{RL}} = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\sqrt {{R^2} + Z_L^2} \)
+ Sử dụng phương pháp khảo sát hàm số.
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
