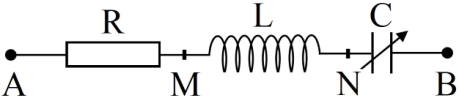
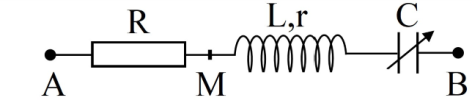Đặt điện áp \(u = {U_0}cos100\pi t\) vào hai đầu đoạn mạch \(AB\) theo thứ tự gồm \(R\), cuộn dây thuần cảm \(L\) và tụ \(C\) nối tiếp. Gọi \(M\) là điểm nối giữa \(R\) và \(L\). Điện áp tức thời của đoạn mạch \(AM\) (chứa R) và \(MB\) (chứa L và C) tại thời điểm \({t_1}\)  là \({u_{AM}} = 60V;{u_{MB}} = 15\sqrt 7 V\) và tại thời điểm \({t_2}\) là \({u_{AM}} = 40\sqrt 3 V;{u_{MB}} = 30V\). Giá trị của \({U_0}\) bằng:

Điện năng được truyền từ đường dây điện một pha có điện áp hiệu dụng ổn định \(220{\rm{ }}V\)vào nhà một hộ dân bằng đường dây tải điện có chất lượng kém. Trong nhà của hộ dân này, dùng một máy biến áp lí tưởng để duy trì điện áp hiệu dụng ở đầu ra luôn là \(220{\rm{ }}V\)(gọi là máy ổn áp). Máy ổn áp này chỉ hoạt động khi điện áp hiệu dụng ở đầu vào lớn hơn \(110{\rm{ }}V\). Tính toán cho thấy, nếu công suất sử dụng điện trong nhà là \(1,1{\rm{ }}kW\) thì tỉ số giữa điện áp hiệu dụng ở đầu ra và điện áp hiệu dụng ở đầu vào (tỉ số tăng áp) của máy ổn áp là\(1,1\) . Coi điện áp và cường độ dòng điện luôn cùng pha. Nếu công suất sử dụng điện trong nhà là \(2,2kW\) thì tỉ số tăng áp của máy ổn áp bằng:

Đặt điện áp xoay chiều $u{\rm{ }} = {\rm{ }}{U_0}cos\omega t$ (${U_0}$ và $\omega $ có giá trị dương, không đổi) vào hai đầu đoạn mạch AB như hình bên, trong đó tụ điện có điện dung C thay đổi được. Biết $R{\rm{ }} = {\rm{ }}5r$, cảm kháng của cuộn dây ${Z_L} = {\rm{ }}4r$ và $CL{\omega ^2} > {\rm{ }}1$. Khi $C{\rm{ }} = {\rm{ }}{C_0}$ và khi $C{\rm{ }} = {\rm{ }}0,5{C_0}$ thì điện áp giữa hai đầu M, B có biểu thức tương ứng là ${u_1} = {\rm{ }}{U_{01}}cos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)$ và ${u_2} = {\rm{ }}{U_{02}}cos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)$ (${U_{01}}$ và ${U_{02}}$ có giá trị dương). Giá trị của $\varphi $ là:

Đặt điện áp \({u_{AB}} = {\rm{ }}30cos100\pi t{\rm{ }}\left( V \right)\) vào hai đầu đoạn mạch \(AB\) như hình bên, trong đó cuộn cảm thuần có độ tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được. Khi \(C{\rm{ }} = {\rm{ }}{C_0}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch \(MN\) đạt giá trị cực đại và điện áp hiệu dụng giữa hai đầu đoạn mạch \(AN\) là \(30\sqrt 2 V\). Khi \(C = 0,5{C_0}\) thì biểu thức điện áp giữa hai đầu cuộn cảm là:

Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có \(R,{\rm{ }}L,{\rm{ }}C\) mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ \(i\). Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích \(u.i\) theo thời gian \(t\). Hệ số công suất của đoạn mạch là:

Điện năng được truyền từ một nhà máy phát điện gồm \(8\) tổ máy đến nơi tiêu thụ bằng đường dây tải điện một pha. Giờ cao điểm cần cả \(8\)  tổ máy hoạt động, hiệu suất truyền tải đạt \(70\% \). Coi điện áp hiệu dụng ở nhà máy không đổi, hệ số công suất của mạch điện bằng \(1\), công suất phát điện của các tổ máy khi hoạt động là không đổi và như nhau. Khi công suất tiêu thụ điện ở nơi tiêu thụ giảm còn \(72,5\% \)  so với giờ cao điểm thì cần bao nhiêu tổ máy hoạt động?

Cho mạch điện như hình vẽ: \(X,{\rm{ }}Y\) là hai hộp, mỗi hộp chỉ chứa $2$ trong $3$ phần tử: điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Ampe kế có điện trở rất nhỏ, các vôn kế có điện trở rất lớn. Các vôn kế và ampe kế đo được cả dòng điện xoay chiều và một chiều. Ban đầu mắc hai điểm $N, D$ vào hai cực của một nguồn điện không đổi thì \({V_2}\) chỉ \(45{\rm{ }}V\), ampe kế chỉ \(1,5{\rm{ }}A\). Sau đó mắc \(M,{\rm{ }}D\) vào nguồn điện xoay chiều có điện áp \(u{\rm{ }} = {\rm{ }}120cos100\pi t{\rm{ }}V\) thì ampe kế chỉ \(1{\rm{ }}A\), hai vôn kế chỉ cùng một giá trị và $u_{MN}$ lệch pha $0,5π $ so với $u_{ND}$. Khi thay tụ $C$ trong mạch bằng tụ $C’$ thì số chỉ vôn kế \({V_1}\)  lớn nhất \({U_{1max}}\) . Giá trị \({U_{1max}}\)  gần giá trị nào nhất sau đây?

Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\)  (\(U\) không đổi, \(\omega \) thay đổi) vào hai đầu đoạn mạch gồm: một điện trở thuần \(R\), một cuộn cảm thuần có độ tự cảm \(L\), một tụ điện có điện \(C\) mắc nối tiếp \(\left( {2L > C{R^2}} \right)\).  Khi \(\omega  = 100\pi \left( {rad/s} \right)\) thì điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại. Khi \(\omega  = 200\pi \left( {rad/s} \right)\) thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cức đại. Giá trị điện áp hiệu dụng cực đại giữa hai đầu cuộn cảm là: