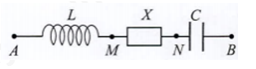
Đặt điện áp \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch AB như hình bên. Trong đó, cuộn cảm thuần có độ tự cảm L; tụ điện có điện dung C; X là đoạn mạch chứa các phần tử có \({R_1},{L_1},{C_1}\) mắc nối tiếp. Biết \(2{\omega ^2}LC = 1\), các điện áp hiệu dụng: \({U_{AN}} = 120V;{U_{MB}} = 90V\), góc lệch pha giữa \({u_{AN}}\) và \({u_{MB}}\)  là  \(\frac{{5\pi }}{{12}}\). Hệ số công suất của X là

Ta có: \(2LC{\omega ^2} = 1 \Leftrightarrow \frac{{2\omega L}}{{\frac{1}{{\omega C}}}} = 1 \Rightarrow 2{Z_L} = {Z_C}\)

\(\begin{array}{l} \Rightarrow 2{u_L} =  - {u_C} \Rightarrow 2{u_L} + {u_C} = 0\\ \Rightarrow 2{u_{AN}} + {u_{MB}} = 2{u_L} + 2{u_X} + {u_X} + {u_C}\\ \Rightarrow 2{u_{AN}} + {u_{MB}} = 3{u_X}\\ \Rightarrow {u_X} = \frac{{2{u_{AN}} + {u_{MB}}}}{3}\end{array}\)

Giả sử \({\varphi _{uMB}} = 0 \Rightarrow {\varphi _{uAN}} = \frac{{5\pi }}{{12}}\)

 \( \Rightarrow \left\{ \begin{array}{l}{u_{MB}} = 90\sqrt 2 \cos \left( {\omega t} \right)\\{u_{AN}} = 120\sqrt 2 .\cos \left( {\omega t + \frac{{5\pi }}{{12}}} \right)\end{array} \right.\)

\(\begin{array}{l} \Rightarrow {u_X} = \frac{{240\sqrt 2 \angle \frac{{5\pi }}{{12}} + 90\sqrt 2 \angle 0}}{3} = 130,7\angle 0,99\\ \Rightarrow {\varphi _{uX}} = 0,99rad\end{array}\)

Lại có: \({u_C} = {u_{MB}} - {u_X} = 122,6\angle  - 1,1\)

\( \Rightarrow {\varphi _i} = {\varphi _{uC}} + \frac{\pi }{2} =  - 1,1 + \frac{\pi }{2} \approx 0,47079rad\)

\( \Rightarrow \) Độ lệch pha giữa \({u_X}\) và \(i\) là:

\({\varphi _X} = {\varphi _{uX}} - {\varphi _i} = 0,99 - 0,47079 = 0,51921rad\)

\( \Rightarrow \) Hệ số công suất của X là:

\(\cos {\varphi _X} = \cos 0,51921 = 0,868\)