Câu hỏi:
2 năm trước
Đặt 4 điện tích âm có cùng độ lớn \(q\) tại 4 đỉnh của một hình vuông ABCD cạnh \(a.\) Xác định cường độ tổng hợp tại giao điểm hai đường chéo của hình vuông.
Trả lời bởi giáo viên
Đáp án đúng: b
Biểu diễn các vecto cường độ điện trường gây ra tại O trên hình vẽ:
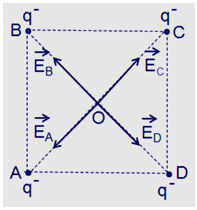
Ta có: \(\overrightarrow {{E_O}} = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} + \overrightarrow {{E_D}} \)
Với: \({E_A} = {E_B} = {E_C} = {E_D} = \dfrac{{k\left| q \right|}}{{O{A^2}}}\)
Do \(\left\{ \begin{array}{l}\overrightarrow {{E_A}} \uparrow \downarrow \overrightarrow {{E_C}} \\{E_A} = {E_C}\end{array} \right. \Rightarrow \overrightarrow {{E_{AC}}} = \overrightarrow {{E_A}} + \overrightarrow {{E_C}} = 0\)
Do \(\left\{ \begin{array}{l}\overrightarrow {{E_B}} \uparrow \downarrow \overrightarrow {{E_D}} \\{E_B} = {E_D}\end{array} \right. \Rightarrow \overrightarrow {{E_{BD}}} = \overrightarrow {{E_B}} + \overrightarrow {{E_D}} = 0\)
Cường độ điện tường tổng hợp tại O là:
\(\overrightarrow {{E_O}} = \left( {\overrightarrow {{E_A}} + \overrightarrow {{E_C}} } \right) + \left( {\overrightarrow {{E_B}} + \overrightarrow {{E_D}} } \right) = 0\)
Hướng dẫn giải:
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
