Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + {m^2}} \right|\) có đúng 5 điểm cực trị?

Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) có \(f'\left( x \right) = 12{x^3} - 12{x^2} - 24x = 12x\left( {{x^2} - x - 2} \right),\)\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 1\\x = 2\end{array} \right.\)

Bảng biến thiên:

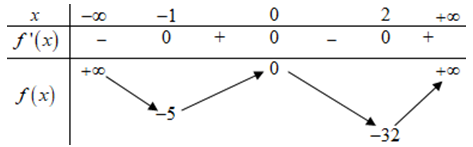
Nhận xét: Hàm số \(f\left( x \right)\) có 3 cực trị là \(x =  - 1,x = 0,x = 2\). Để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + {m^2}} \right| = \left| {f\left( x \right) + {m^2}} \right|\) có đúng 5 cực trị thì đường thẳng \(y =  - {m^2}\) hoặc cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm phân biệt, khác các điểm cực trị hoặc cắt đồ thị hàm số tại 3 điểm phân biệt, trong đó có 1 điểm cực trị.

\( \Leftrightarrow \left[ \begin{array}{l} - {m^2} \ge 0\\ - 32 \le  - {m^2} \le  - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\\sqrt 5  \le \left| m \right| \le \sqrt {32} \end{array} \right.\)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;3;4;5; - 3; - 4; - 5} \right\}\): có 7 giá trị thỏa mãn.