Cho tứ diện \(SABC\) và \(G\) là trọng tâm của tứ diện, mặt phẳng quay quanh \(AG\) và cắt các cạnh \(SB,\,SC\) tương ứng tại \(M,\,N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}}\) là
Trả lời bởi giáo viên
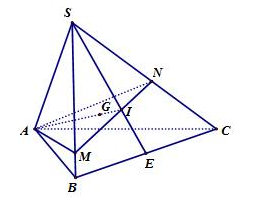
Đặt \(\dfrac{{SM}}{{SB}} = a;\,\dfrac{{SN}}{{SC}} = b\,\,\left( {0 < a;b < 1} \right)\)
Lấy \(E\) là trung điểm \(BC\).
Trong \(\left( {SAE} \right)\), kéo dài \(AG\) cắt \(SE\) tại \(I\). Khi đó \(I \in MN\) và \(I\) là trọng tâm tam giác \(SBC.\)
Khi đó trong tam giác \(SBC\) ta luôn có \(\dfrac{{SB}}{{SM}} + \dfrac{{SC}}{{SN}} = 3\) (tính chất đã được chứng minh ở trên)
Lại có \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = ab\)
Ta có \(\dfrac{{SB}}{{SM}} + \dfrac{{SC}}{{SN}} = 3\) \( \Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} = 3.\)
Xét \(\dfrac{1}{a} + \dfrac{1}{b}\mathop \ge \limits^{Cô - si} \dfrac{2}{{\sqrt {ab} }} \Leftrightarrow \sqrt {ab} \ge \dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}} = \dfrac{2}{3} \Leftrightarrow ab \ge \dfrac{4}{9}\)
Dấu = xảy ra khi \(a = b = \dfrac{2}{3}\) .
Từ đó \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = ab \ge \dfrac{4}{9}\) hay tỉ số \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}}\) nhỏ nhất là bằng \(\dfrac{4}{9}.\)
Hướng dẫn giải:
+ Sử dụng tỉ số thể tích: Cho chóp tam giác \(S.ABC\) có \(M \in SA,N \in SB,P \in SC \Rightarrow \dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}\)
+ Sử dụng tính chất: Cho tam giác \(ABC\) có trọng tâm \(G.\) Đường thẳng bất kì đi qua \(G\) cắt các cạnh \(AB,AC\) làn lượt tại \(M,N\). Khi đó ta có \(\dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = 3.\)
(Chứng minh tính chất trên như sau:
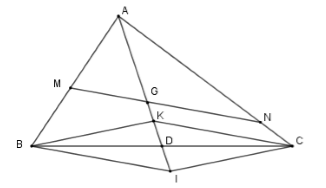
Qua B, C kẻ các đường thẳng song song với \(MN\) cắt đường thẳng \(AG\) tại \(K\) và \(I.\) Gọi \(D\) là trung điểm \(BC.\)
Theo định lý Ta-lét ta có \(\dfrac{{AB}}{{AM}} = \dfrac{{AI}}{{AG}};\dfrac{{AC}}{{AN}} = \dfrac{{AK}}{{AG}} \Rightarrow \dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = \dfrac{{AI}}{{AG}} + \dfrac{{AK}}{{AG}} = \dfrac{{AI + AK}}{{AG}}\)
Mà \(\Delta IBD = \Delta KCD\left( {g - c - g} \right) \Rightarrow KD = ID\)
\( \Rightarrow AI + AK = AD + DI + AK = AD + KD + AK = AD + AD = 2AD = 2.\dfrac{3}{2}AG = 3AG\)
Do đó \(\dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = \dfrac{{AI + AK}}{{AG}} = \dfrac{{3AG}}{{AG}} = 3.\) )
+ Sử dụng bất đẳng thức Cô-si để tìm giá trị nhỏ nhất.
+ Lưu ý rằng trọng tâm tứ diện là giao của 4 đường thẳng nối đỉnh và trọng tâm tam giác đối diện.

