Câu hỏi:
2 năm trước
Cho tứ diện \(SABC\). Gọi \(L,{\rm{ }}M,{\rm{ }}N\) lần lượt là các điểm trên các cạnh \(SA,{\rm{ }}SB\) và \(AC\) sao cho \(LM\) không song song với \(AB\), \(LN\) không song song với \(SC\). Mặt phẳng \(\left( {LMN} \right)\) cắt các đường thẳng \(AB,{\rm{ }}BC,{\rm{ }}SC\) lần lượt tại \(K,{\rm{ }}I,{\rm{ }}J\). Ba điểm nào sau đây thẳng hàng?
Trả lời bởi giáo viên
Đáp án đúng: b
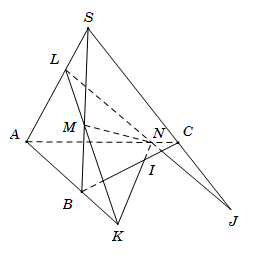
Ta có
● \(M \in SB\) suy \(M\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
● \(I\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
● \(J\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
Vậy \(M,{\rm{ }}I,{\rm{ }}J\) thẳng hàng vì cùng thuộc giao tuyến của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
Hướng dẫn giải:
- Tìm \(d = \left( {LMN} \right) \cap \left( {SBC} \right)\).
- Chứng minh \(d\) đi qua ba điểm \(M,I,J \in d\).
