Câu hỏi:
2 năm trước
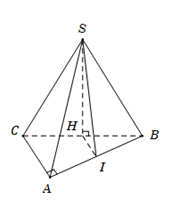
Cho tứ diện $SABC$ có $SBC$ và $ABC$ nằm trong hai mặt phẳng vuông góc với nhau. Tam giác $SBC$ đều, tam giác $ABC$ vuông tại $A$. Gọi $H$, $I$ lần lượt là trung điểm của $BC$ và $AB$. Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: c
Do $SBC$ là tam giác đều có $H$ là trung điểm $BC$ nên $SH \bot BC$.
Mà $\left( {SBC} \right) \bot \left( {ABC} \right)$ theo giao tuyến $BC \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot AB.$
\( \Rightarrow \) Đáp án A đúng.
Ta có $HI$ là đường trung bình của $\Delta \,ABC$ nên $HI\parallel AC \Rightarrow HI \bot AB.$
\( \Rightarrow \) Đáp án B đúng.
Ta có $\left\{ \begin{array}{l}SH \bot AB\\HI \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SHI} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SHI} \right).$
\( \Rightarrow \) Đáp án D đúng.
Dùng phương pháp loại trừ thì C là đáp án sai.
