Câu hỏi:
2 năm trước
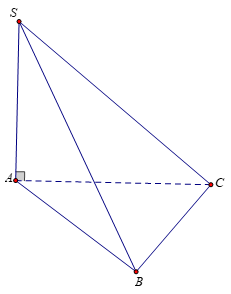
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),\) tam giác \(ABC\) vuông tại \(B\), kết luận nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: a
+) Nếu đáp án A đúng: \(\left( {SAC} \right) \bot \left( {SAB} \right)\)
Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\)
Mà SA là giao tuyến của hai mặt phẳng vuông góc \(\left( {SAC} \right) \bot \left( {SAB} \right)\) \( \Rightarrow AB \bot \left( {SAC} \right) \Rightarrow AB \bot AC\) (Vô lý vì tam giác ABC vuông tại B.)
Vậy A sai.
+) Ta có: \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\SA \subset \left( {SAB} \right),\left( {SAC} \right)\end{array} \right.\) \( \Rightarrow \) \(\left( {SAB} \right),\,\left( {SAC} \right) \bot \left( {ABC} \right)\) \( \Rightarrow \) B, C đúng.
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\) mà \(BC \bot AB\) \( \Rightarrow \) \(BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right)\)
\( \Rightarrow \) \(\left( {SAB} \right) \bot \left( {SBC} \right)\) \( \Rightarrow \) D đúng.
Hướng dẫn giải:
Xét tính đúng sai của từng đáp án, sử dụng lý thuyết: Nếu một đường thẳng vuông góc với một mặt phẳng thì mọi mặt phẳng chứa đường thẳng đều vuông góc với mặt phẳng đã cho.
Xét đáp án A: Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến đều vuông góc với mặt phẳng kia.
