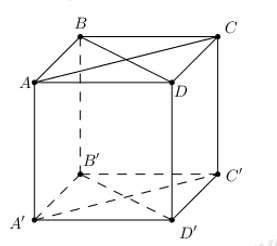
Cho hình hộp đứng \(ABCD.A'B'C'D’\) . Xét tất cả các hình bình hành có đỉnh là đỉnh của hình hộp đó. Hỏi có bao nhiêu hình bình hành mà mặt phẳng chứa nó vuông góc với mặt phẳng đáy \( (ABCD)\) ?

$2.$

$3.$     

$1.$

Vô số

Cho hai đường thẳng song song $a$ và $b$ và đường thẳng $c$ sao cho $c \bot a,\;\,c \bot b$. Mọi mặt phẳng $\left( \alpha  \right)$ chứa $c$ thì đều vuông góc với mặt phẳng $\left( {a,b} \right)$.

Cho $a \bot \left( \alpha  \right)$, mọi mặt phẳng $\left( \beta  \right)$ chứa $a$ thì $\left( \beta  \right) \bot \left( \alpha  \right)$.

Cho $a \bot b$, mọi mặt phẳng chứa $b$ đều vuông góc với $a$.

Cho $a \bot b$, nếu $a \subset \left( \alpha  \right)$ và $b \subset \left( \beta  \right)$ thì $\left( \alpha  \right) \bot \left( \beta  \right)$.

Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.

Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước

 Ba mặt phẳng \(\left( ABC \right),\,\,\left( ABD \right),\,\,\left( ACD \right)\) đôi một vuông góc.

Hình chiếu của A lên mặt phẳng \(\left( BCD \right)\) là trực tâm của tam giác BCD.

Tam giác BCD vuông.

 Hai cạnh đối của tứ diện vuông góc.

\(\left( {SAC} \right) \bot \left( {SAB} \right)\).

\(\left( {SAB} \right) \bot \left( {ABC} \right)\)

\(\left( {SAC} \right) \bot \left( {ABC} \right)\).

\(\left( {SAB} \right) \bot \left( {SBC} \right)\).

$BM \bot AC.$

$\left( {SBM} \right) \bot \left( {SAC} \right).$       

$\left( {SAB} \right) \bot \left( {SBC} \right).$

$\left( {SAB} \right) \bot \left( {SAC} \right).$