Câu hỏi:
2 năm trước
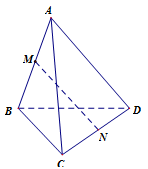
Cho tứ diện ABCD, M và N theo thứ tự là trung điểm của AB và CD. Bộ ba vecto nào dưới đây đồng phẳng?
Trả lời bởi giáo viên
Đáp án đúng: c
→AD=→AM+→MN+→ND→BC=→BM+→MN+→NC⇒→AD+→BC=2→MN⇒→MN=12→AD+12→BC
Vậy ba vecto →BC;→AD;→MN đồng phẳng.
Hướng dẫn giải:
Ba véc tơ →a,→b,→c đồng phẳng ⇔∃m,n sao cho →c=m.→a+n.→b (.m,n. là duy nhất).

