Cho tứ diện \(ABCD.\) Gọi \(G\) là trực tâm của tam giác \(BCD.\) Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\)là:
Trả lời bởi giáo viên
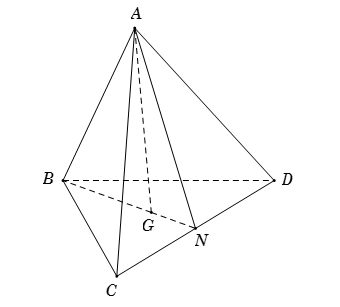
\( \bullet \) \(A\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
\( \bullet \) Ta có \(BG \cap CD = N\) \( \Rightarrow \left\{ \begin{array}{l}N \in BG \subset \left( {ABG} \right) \Rightarrow N \in \left( {ABG} \right)\\N \in CD \subset \left( {ACD} \right) \Rightarrow N \in \left( {ACD} \right)\end{array} \right.\)
\( \Rightarrow N\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
Vậy \(\left( {ABG} \right) \cap \left( {ACD} \right) = AN.\)
Mà \(G\) là trực tâm của tam giác \(\Delta BCD\) nên \(BG \bot CD\) tại \(N\) hay \(N\) là hình chiếu của \(B\) lên \(CD\).
Hướng dẫn giải:
- Xác định giao tuyến của hai mặt phẳng bằng cách xác định hai điểm chung của chúng.

