Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
Trả lời bởi giáo viên
Đáp án đúng: b
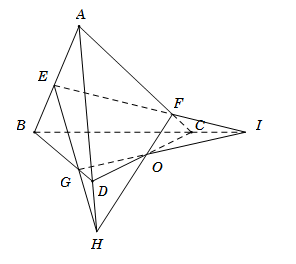
Trong $mp(EHI)$, gọi \(O = HF \cap IG\). Ta có
● \(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\).
● \(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\).
Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\).
Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
Hướng dẫn giải:
Để chứng minh ba đường thẳng \({d_1},{\rm{ }}{d_2},{\rm{ }}{d_3}\) đồng quy ta chứng minh giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\) là điểm chung của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\); đồng thời \({d_3}\) là giao tuyến \(\left( \alpha \right)\) và \(\left( \beta \right)\).
