Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AB\) vuông góc với \(CD\), \(AB = CD = 6\). \(M\) là điểm thuộc cạnh \(BC\) sao cho \(MC = x.BC{\rm{ }}\left( {0 < x < 1} \right)\). Mặt phẳng\(\left( P \right)\) song song với \(AB\) và \(CD\) lần lượt cắt \(BC,DB,AD,AC\) tại \(M,N,P,Q\). Diện tích lớn nhất của tứ giác bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
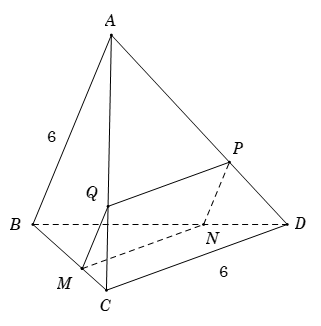
Xét tứ giác \(MNPQ\) có \(\left\{ \begin{array}{l}MQ{\rm{//}}NP{\rm{//}}AB\\MN{\rm{//}}PQ{\rm{//}}CD\end{array} \right.\)\( \Rightarrow MNPQ\) là hình bình hành.
Mặt khác, \(AB \bot CD \Rightarrow MQ \bot MN\). Do đó, \(MNPQ\) là hình chữ nhật.
Vì \(MQ{\rm{//}}AB\) nên \(\dfrac{{MQ}}{{AB}} = \dfrac{{CM}}{{CB}} = x \Rightarrow MQ = x.AB = 6x\).
Theo giả thiết \(MC = x.BC \Rightarrow BM = \left( {1 - x} \right)BC\).
Vì \(MN{\rm{//}}CD\) nên \(\dfrac{{MN}}{{CD}} = \dfrac{{BM}}{{BC}} = 1 - x \Rightarrow MN = \left( {1 - x} \right).CD = 6\left( {1 - x} \right)\).
Diện tích hình chữ nhật \(MNPQ\) là
\({S_{MNPQ}} = MN.MQ = 6\left( {1 - x} \right).6x = 36.x.\left( {1 - x} \right) \le 36{\left( {\dfrac{{x + 1 - x}}{2}} \right)^2} = 9\) .
Ta có \({S_{MNPQ}} = 9\) khi \(x = 1 - x \Leftrightarrow x = \dfrac{1}{2}\) .
Vậy diện tích tứ giác \(MNPQ\) lớn nhất bằng \(9\) khi \(M\) là trung điểm của \(BC\).
Hướng dẫn giải:
- Xác định thiết diện.
- Nhận xét tính chất thiết diện và tính diện tích theo \(x\).
- Tìm GTNN của diện tích theo \(x\) và kết luận.
Câu hỏi khác
- Bài tập phần hai đường thẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần góc giữa đường thẳng và mặt phẳng thi ĐGTD Bách khoa
- Bài tập phần hai mặt phẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần đường thẳng vuông góc với mặt phẳng thi ĐGTD Bách khoa
- Bài tập góc giữa hai mặt phẳng môn toán ĐGNL có lời giải
