Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
Trả lời bởi giáo viên
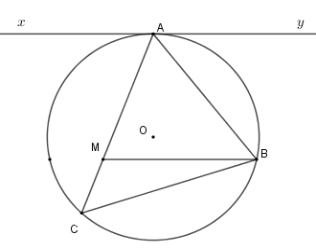
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .
Hướng dẫn giải:
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
Câu hỏi khác
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |