Câu hỏi:
2 năm trước
Cho tam giác $MNP$ cân ở $M,$ trung tuyến $MA,$ trọng tâm $G.$ Biết $MN = 13cm,\;NA = 12cm.$ Khi đó độ dài $MG$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
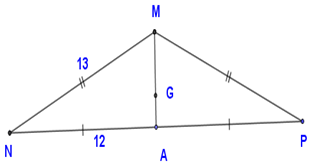
Vì $\Delta MNP$ cân tại $M$ có $MA$ là trung tuyến nên $MA$ cũng là đường cao (tính chất các đường trong tam giác cân)
Xét $\Delta MAN\;$ vuông tại $A$, theo định lý Pytago ta có: \(M{A^2} + N{A^2} = M{N^2} \Leftrightarrow M{A^2} = M{N^2} - N{A^2} = {13^2} - {12^2} = 25 \Rightarrow MA = 5cm\)
Vì $MA$ là trung tuyến, $G\;$ là trọng tâm nên theo tính chất trọng tâm tam giác ta có \(MG = \dfrac{2}{3}MA = \dfrac{2}{3}.5 = \dfrac{{10}}{3}\,cm\)
Hướng dẫn giải:
Bước 1: Tính $MA$ dựa vào định lý Pitago.
Bước 2: Tính $MG$ dựa vào tính chất trọng tâm.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
