Câu hỏi:
2 năm trước
Cho tam giác đều $ABC$ cạnh $a$. Gọi $D$ là điểm đối xứng với $A$ qua $BC$. Trên đường thẳng vuông góc với mặt phẳng $\left( {ABC} \right)$ tại $D$ lấy điểm $S$ sao cho $SD = \dfrac{{a\sqrt 6 }}{2}$. Gọi $I$ là trung điểm $BC$; kẻ $IH$ vuông góc $SA$ $\left( {H \in SA} \right)$. Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: b
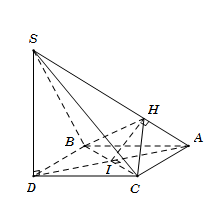
Từ giả thiết suy ra $ABDC$ là hình thoi nên $BC \bot AD.$
Ta có $\left\{ \begin{array}{l}BC \bot AD\\BC \bot SD\end{array} \right. \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SA$.
Lại có theo giả thiết $IH \bot SA$. Từ đó suy ra $SA \bot \left( {HCB} \right) \Rightarrow SA \bot BH$.
\( \Rightarrow \) Đáp án A đúng.
Tính được $AI = \dfrac{{a\sqrt 3 }}{2}$, $AD = 2AI = a\sqrt 3 $, $S{A^2} = \sqrt {A{D^2} + S{D^2}} = \dfrac{{3a\sqrt 2 }}{2}.$
Ta có $\Delta AHI \sim \Delta ADS \Rightarrow \dfrac{{IH}}{{SD}} = \dfrac{{AI}}{{AS}} \Rightarrow IH = \dfrac{{AI.SD}}{{AS}} = \dfrac{a}{2} = \dfrac{{BC}}{2} \Rightarrow $ Tam giác $HBC$ có trung tuyến $IH$ bằng nửa cạnh đáy $BC$ nên $\widehat {BHC} = {90^0}$ hay $BH \bot HC$. Do đó D đúng.
Từ mệnh đề A và D suy ra \(BH \bot \left( {SAC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SAC} \right) \Rightarrow \) mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
