Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\)
Tính số đo góc \(DBK.\)
Trả lời bởi giáo viên
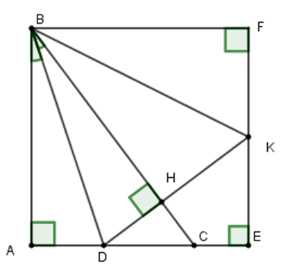
+ Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\)
Khi đó ta có \(ABFE\) là hình vuông nên \(\widehat {ABF} = 90^\circ \) và \(AB = BF\)
Lại có \(AB = BH\) (ý trước) nên \(BH = BF\)
Xét hai tam giác vuông \(BHK\) và \(BFK\) có \(BH = BF\left( {cmt} \right);\,BK\) cạnh chung
Nên \(\Delta BHK = \Delta BFK\left( {ch - cgv} \right)\)\( \Rightarrow \widehat {FBK} = \widehat {HBK}\)
Lại có \(\widehat {ABD} = \widehat {DBH}\) (do \(BD\) là phân giác góc \(\widehat {ABC}\) )
Nên \(\widehat {DBH} + \widehat {HBK} = \widehat {ABD} + \widehat {KBF} = \dfrac{{\widehat {DBH} + \widehat {HBK} + \widehat {ABD} + \widehat {KBF}}}{2}\)\(\dfrac{{\widehat {ABF}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Mà Vậy \(\widehat {DBK} = \widehat {DBH} + \widehat {HBK} = 45^\circ .\)
Hướng dẫn giải:
+ Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\)
+ Suy ra \(\widehat {ABF} = 90^\circ \) và \(AB = BF\)
+Chứng minh \(\widehat {KBH} = \widehat {FBK}\) (dựa vào hai tam giác bằng nhau)
+ Lập luận để suy ra số đo góc \(DBK.\)

